קטע אמצעים במשולש וטרפז שווה שוקיים - תרגיל פתור

שאלה

EF הוא קטע אמצעים בטרפז שווה שוקיים ABCD.

AH הוא גובה בטרפז והוא חותך את הקטע EF בנקודה G. 

נתון:  ס״מ EF =  25  , ס״מ DH =  10.

א. חשב את EG.

ב. חשב את הבסיסים AB ו- DC.

פתרון

הוכחת סעיף א 

EF קטע אמצעים בטרפז ABCD ומקביל ל - DC

מהקטע אמצעים אנחנו יודעים ש- AE=ED
לכן EG קטע אמצעים במשולש ADH כי הוא חוצה צלע אחת AD ומקביל לצלע השלישית DH (חלקי קטעים מקבילים) .

נתון כי DH=10

לכן EG=5 -(קטע האמצעים EG במשולש ADH שווה למחצית הבסיס DH)

מ.ש.ל סעיף א

הוכחת סעיף ב

 

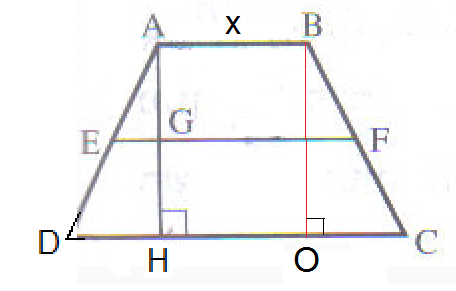
בונים בניית עזר אנך מנקודה B ל- DC בנקודה O.
במרובע ABOH כל הזויות ישרות ולכן הוא מלבן. שבו AB = HO נסמן שווה ל- x. (כלומר AB=HO=x)

מאחר והטרפז שווה שוקיים המשולשים ADH ו- BCO חופפים:
שיוויון השוקיים AD= BC, שיוויון צלעות המלבן AH = B, ושיוויון זויות DAH, CBO (הפרשי זויות זויות שוות מזויות שוות).

מהחפיפה נובע: DH = CO = 10
סכום שני בסיסי הטרפז: AB + CD = x +10 +x + 10 = 2x + 20

אך גם סכום בסיסי הטרפז שווה לפעמיים קטע האמצעים EF או ל:  2ᐧ 25 = 50

לכן: 2x + 20 = 50

אורך בסיס קטן x= 15 : AB

ואורך בסיס גדול CD = 10 + 10 + 15 = 35

מ.ש.ל סעיף ב