משפט: אם שני ישרים מקבילים נחתכים על-ידי ישר שלישי, אזי כל שתי זוויות מתאימות הן זהות
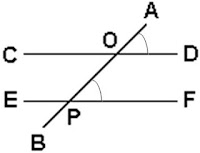
נתון: שני ישרים מקבילים: CD||EF , ישר AP חותך את המקבילים בנקודות O, P
נתון: שני ישרים מקבילים: CD||EF , ישר AP חותך את המקבילים בנקודות O, P
צ"ל: AOD = ∡OPF∡
| טענה | נימוק | |
|---|---|---|
| ∡AOD + 180º = ∡DOP | (1) | סכום שתי זוויות צמודות הוא 180º |
| ∡OPF + 180º = ∡DOP | (2) | סכום שתי זוויות פנימיות וחד-צדדיות בישרים מקבילים |
| ∡AOD+∡DOP + ∡OPF=∡DOP | (3) | שני גדלים השווים לגודל שלישי שווים ביניהם, טענות 1 ו- 2 |
| AOD = ∡OPF ∡
| (4) | חישוב מטענה |

אין תגובות:
הוסף רשומת תגובה