ישר היוצא ממרכז המעגל וחוצה מיתר, מאונך למיתר - הוכחה

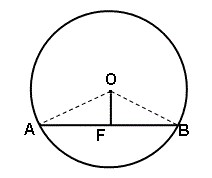
מוכיחים שמשולש AOB שווה שוקיים ע"י שוויון צלעות AO ו- BO (רדיוסים), ובמשולש שווה שוקיים התיכון (OF) לבסיס (AB) מאונך לו. 

נתון:

מעגל שמרכזו O,

 AF = FB 

צ"ל

 OF מאונך ל- AB.

הוכחה

1. AO = BO  - רדיוסים במעגל שווים

2. משולש AOB שווה שוקיים - שוקיים AO, BO שוות (לפי 1)

3. AF = FB - נתון

4. OF מאונך ל- AB - במשולש שווה שוקיים התיכון לבסיס הוא גם גובה (לפי 2, 3)

מ.ש.ל