הניצב במשולש ישר זווית הוא הממוצע הגאומטרי של היתר והיטלו של ניצב זה על היתר - משפט אוקלידס

הוכחת משפט בגאומטריה: הניצב במשולש ישר זווית הוא הממוצע הגאומטרי של היתר והיטלו של ניצב זה על היתר

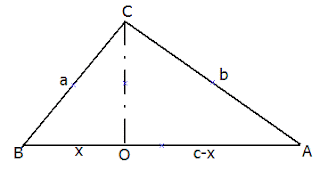משולש ישר זווית ABC, זווית C ישרה

נתון

משולש ישר זוית ABC שבו: 90° =  C⦠.

CO גובה ליתר AB בנקודה O.

נסמן :

AO = c - x , BO = x , CO = h , AB = c (ראו איור לעיל)

צריך להוכיח:   (a = √(cx

הוכחה:

משפט פיתגורס במשולש BCO:

a² - x² = h²

משפט פיתגורס במשולש ACO:

b² - (c - x)² = h²

מכאן:

b² - (c - x)² = a² - x² 

משפט פיתגורס במשולש ABC:

a² + b² = c²  

נחלץ את  b²  משתי משוואות:

b²  = (c - x)² + (a² - x²)

b² = c²  - a² 

לכן:

c²  - a²  = (c - x)² + (a² - x²)

נפתח:

c²  - a²  = c² - 2cx + x² +  a² - x² 

3cx = 2a² 

a²  = cx

a = √(cx)

מ.ש.ל