מבחן מיצב כיתה ח תשס"א פתרונות שאלות 13-15

שאלה מספר 13

פִּתרו את המשוואה שלפניכם, הציגו את דרך הפתרון:

(2x + 8) / 6 - x = (x + 10) / 3

פתרון שאלה 13

(2x + 8) / 6 - x = (x + 10) / 3

כופלים כל האגפים ב- 6:

2x + 8 - 6x = 2(x + 10)
2x + 8 - 6x = 2x + 20
6x = -12

x = -2

שאלה מספר 14

פתרון שאלה 14

הוכחה

1. - נובע מחפיפת משולשים ABC, AFD
2 . - נתון
3. - נובע מ- 1 ו-2 , בהצבה
נתבונן בזויות המשולש AFD, סכומן 180 מעלות, לכן:

4. - סכום זויות במשולש הוא 180 מעלות
5. אך זויות FAD, AFD שוות 25 , 80 מעלות בהתאמה - נתון והוכח ב- 3
6. מכאן זוית ADF שווה 180-80-25 = 75 מעלות - נובע מ-4 , 5

שאלה מספר  15 - שיפוע גרף ישר ומציאת משוואת הישר

לפניכם גרף המתאר את הפונקציה הקווית f.

א. מה שיפוע הישר?

תשובה _______________ 

 

ב. כתבו פונקציה g שהגרף המתאר אותה הוא ישר המקביל לגרף הפונקציה f , 

ועובר דרך הנקודה (12 , 0).

פתרון שאלה 15

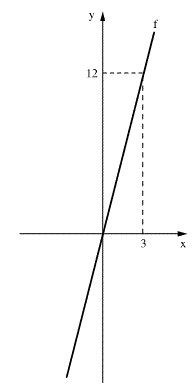
סעיף א - משוואת הפונקציה הקווית f היא y = ax +b כאשר a הוא שיפוע הגרף ו- b היא נקודת חיתוך עם ציר y.
במקרה לפנינו הגרף עובר דרך ראשית הצירים נקודה (0,0) ולכן b =0 .
הגרף עובר גם דרך הנקודה (3,12) ולכן נציב המשוואה y = ax ונקבל 12 = 3a , או a = 4 , כלומר שיפוע הגרף הוא 4.
סעיף ב - הפונקציה g היא גרף ישר המקבילה ל- f , לכן יש לה אותו שיפוע a = 4 . נקודת חיתוך של g עם ציר y היא (0,12) לכן b = 12.
משוואת פונקציית הישר g היא מהצורה: y = ax +b , כלומר: y = 4x +12
שרטוט הפונקציות f,g: ( הפונק' g בצבע כחול)

שרטוט הפונקציות f,g: ( הפונק' g בצבע כחול)

שאלה 16

גנן תכנן להרכיב צינור מים מארבעה חלקים, ולהניח אותו בגינה שאורכה 5 מטרים.

האורך הכולל של הצינור צריך להיות קצר מאורך הגינה.

הגנן הניח חלק אחד שאורכו 2.3 מטרים, וחיבר אליו עוד שלושה חלקים אחרים השווים באורכם זה לזה, כפי שמתואר בסרטוט. x מייצג את האורך במטרים של כל אחד משלושת החלקים השווים באורכם.

 
א. כִּתבו שני אורכים אפשריים שונים לחלק של הצינור שאורכו מיוצג על ידי x.

פתרון סעיף 16.א

אורך כל החלקים יחד צריך להיות קטן מ-5 מ', כלומר הסכום של החלק האחד באורך 2.3 מ' ועוד 3 חלקים שווים באורך x קטן מ- 5 מ'.
ניתן לתאר את השאלה באי שיוויון: 

2.3 + 3x < 5

נפתור את אי השיוויון:

2.3 + 3x < 5
3x < 5 - 2.3
3x < 2.7

x < 0.9

x חייב להיות קטן מ- 0.9 מ'.
אורכים אפשריים ל- x : 
0.8מ', 0.6 מ'.


ב. סַמנו את האי-שוויון המתאים לנתוני השאלה.

 

 פתרון סעיף 16.ב

תשובה: כפי שענינו בסעיף 1 לעיל התשובה הנכונה היא 2:

2.3 + 3x < 5