משוואות דיפרנציאליות משמשות פעמים רבות לפתרון בעיות באמצעות מודל מתמטי, להלן דוגמא.
המיכל בתמונה מכיל בתחילה 1000 ליטר מים שבהם מומסים 100 גרם מלח.
לתוך המיכל נכנסים 10 ליטר מים לדקה שבהם מומסים 5 גרם מלח לליטר. התערובת במיכל אחידה.
מתוך המיכל יוצאים 10 ליטר מים לדקה.
חשב את כמות המלח במיכל כפונקציה של הזמן.
פתרון:
נסמן ב- y(t) את כמות המלח במיכל כפונקציה של הזמן.
'y הוא קצב השתנות כמות המלח ושווה לכמות המלח הנכנסת למיכל פחות כמות המלח שיוצאת ממנו:
כמות המלח שנכנסת למיכל היא 10 ליטר מים לדקה שנכנסים למיכל כפול 5 גרם מלח לליטר כלומר 50 גרם מלח לדקה.
כמות המלח שיוצאת מהמיכל היא הכמות המומסת ב - 10 ליטר מים במיכל כלומר ( 10/1000 * y )
לכן המודל למשוואה הדיפרנציאלית:
,תנאי התחלה הוא כמות המלח במיכל בתחילת התהליך :
נפתור את המשוואה הדיפרנציאלית בעזרת הפרדת משתנים.

למציאת קבוע האינטגרציה c נציב את תנאי ההתחלה y(0) = 100
ונקבל
ולכן כמות המלח y במיכל כפונקציה של הזמן:

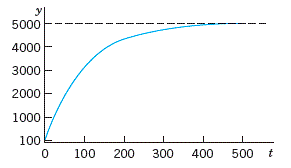
ניתן לתאר את כמות המלח במיכל בצורה גרפית, כאשר t שואף לאינסוף כמות המיכל תגיע ל - 5000 גרם (1000 ליטר במיכל מוכפל בריכוז המלח בזרם המים שנכנס 5 גרם לליטר)
15
המיכל בתמונה מכיל בתחילה 1000 ליטר מים שבהם מומסים 100 גרם מלח.
לתוך המיכל נכנסים 10 ליטר מים לדקה שבהם מומסים 5 גרם מלח לליטר. התערובת במיכל אחידה.
מתוך המיכל יוצאים 10 ליטר מים לדקה.
חשב את כמות המלח במיכל כפונקציה של הזמן.
 |
| מיכל |
נסמן ב- y(t) את כמות המלח במיכל כפונקציה של הזמן.
'y הוא קצב השתנות כמות המלח ושווה לכמות המלח הנכנסת למיכל פחות כמות המלח שיוצאת ממנו:
כמות המלח שנכנסת למיכל היא 10 ליטר מים לדקה שנכנסים למיכל כפול 5 גרם מלח לליטר כלומר 50 גרם מלח לדקה.
כמות המלח שיוצאת מהמיכל היא הכמות המומסת ב - 10 ליטר מים במיכל כלומר ( 10/1000 * y )
לכן המודל למשוואה הדיפרנציאלית:
,תנאי התחלה הוא כמות המלח במיכל בתחילת התהליך :
נפתור את המשוואה הדיפרנציאלית בעזרת הפרדת משתנים.
למציאת קבוע האינטגרציה c נציב את תנאי ההתחלה y(0) = 100
ונקבל
ולכן כמות המלח y במיכל כפונקציה של הזמן:
ניתן לתאר את כמות המלח במיכל בצורה גרפית, כאשר t שואף לאינסוף כמות המיכל תגיע ל - 5000 גרם (1000 ליטר במיכל מוכפל בריכוז המלח בזרם המים שנכנס 5 גרם לליטר)
 |
| מלח במיכל - y |

אין תגובות:
הוסף רשומת תגובה