מתוך מבחן מפמ"ר לכיתה ז , 2010
שאלה 21
פתרון שאלה 21
א.
הוכחה - זוית B1 ישרה
1: - זויות המלבן ישרות וזוית ABC היא זוית במלבן ABCD
- זויות המלבן ישרות וזוית ABC היא זוית במלבן ABCD
2: - זויות ABC, B1 הן זויות צמודות על ישר AK ולכן סכומן 180 מעלות
- זויות ABC, B1 הן זויות צמודות על ישר AK ולכן סכומן 180 מעלות
3: - הצבת 1 ב- 2
- הצבת 1 ב- 2
4: - נובע מ- 3
- נובע מ- 3
מ.ש.ל
ב.
הוכחה - זוית LPB ישרה
5: AK||ML - צלעות נגדיות במלבן AKLM מקבילות
6: - נובע מ- 5 - זויות פנימיות מתחלפות בין מקבילים שוות (מקבילים AK||ML, חותך: BP)
- נובע מ- 5 - זויות פנימיות מתחלפות בין מקבילים שוות (מקבילים AK||ML, חותך: BP)
7: - הצבת 1 (מהוכחה סעיף א) ב- 6
- הצבת 1 (מהוכחה סעיף א) ב- 6
מ.ש.ל
שאלה 22
נתון מלבן ABCD. הנקודה E אמצע הקטע AB, חיברו את הנקודה E עם קודקודי המלבן C, D.
שאלה 21
פתרון שאלה 21
א.
הוכחה - זוית B1 ישרה
1:
2:
3:
4:
מ.ש.ל
ב.
הוכחה - זוית LPB ישרה
5: AK||ML - צלעות נגדיות במלבן AKLM מקבילות
6:
7:
מ.ש.ל
שאלה 22
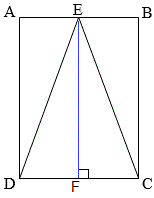
נתון מלבן ABCD. הנקודה E אמצע הקטע AB, חיברו את הנקודה E עם קודקודי המלבן C, D.
א. נמקו מדוע משולש DEC הוא משולש שווה שוקיים, כלומר ED = EC
ב. פי כמה גדול שטח המלבן ABCD משטח המשולש DEC?
תשובה: פי ______
פתרון שאלה 22
א. משולש DEC הוא משולש שווה שוקיים, כלומר ED = EC
השיטה: חופפים משולשים EBC, EAD ע"י שוויון צלעות המלבן ABCD, הצלעות AD=DC, שיוויון הזויות הישרות A,B ושיוויון הקטעים AE=BE. מחפיפת משולשים EAD, EBC נובע שיוויון הצלעות EC=ED.
הוכחה:
חפיפת משולשים EBC, EAD
1: AD = BC - צלעות נגדיות במלבן (ABCD) שוות
2: זוית B = זוית C - זוויות המלבן (ABCD) ישרות ולכן גם שוות
3: AE= BE - נתון
4: משולשים EBC, EAD חופפים - נובע מ- 1,2,3 צ.ז.צ
5: EC = ED - נובע מהחפיפה, הצלעות מול הזוויות השוות B,A
לכן משולש DEC הוא משולש שווה שוקיים.
מ.ש.ל
ב. פי כמה גדול שטח המלבן ABCD משטח המשולש DEC?
ב. פי כמה גדול שטח המלבן ABCD משטח המשולש DEC?
תשובה: פי ______
פתרון שאלה 22
א. משולש DEC הוא משולש שווה שוקיים, כלומר ED = EC
השיטה: חופפים משולשים EBC, EAD ע"י שוויון צלעות המלבן ABCD, הצלעות AD=DC, שיוויון הזויות הישרות A,B ושיוויון הקטעים AE=BE. מחפיפת משולשים EAD, EBC נובע שיוויון הצלעות EC=ED.
הוכחה:
חפיפת משולשים EBC, EAD
1: AD = BC - צלעות נגדיות במלבן (ABCD) שוות
2: זוית B = זוית C - זוויות המלבן (ABCD) ישרות ולכן גם שוות
3: AE= BE - נתון
4: משולשים EBC, EAD חופפים - נובע מ- 1,2,3 צ.ז.צ
5: EC = ED - נובע מהחפיפה, הצלעות מול הזוויות השוות B,A
לכן משולש DEC הוא משולש שווה שוקיים.
מ.ש.ל
ב. פי כמה גדול שטח המלבן ABCD משטח המשולש DEC?
השיטה: בונים בניית עזר גובה למשולש DEC מקודקוד E לצלע CD שחותך אותה בנקודה F. מוכיחים שגובה המשולש EF שווה לגובה BC של המלבן ABCD, ומאחר ולמשולש DEC ולמלבן ABCD אותו בסיס CD אזי שטח המשולש שווה מחצית שטח המלבן.
הוכחה:
1: השטח S של מלבן ABCD שווה מכפלת גובהו BC בבבסיסו CD כלומר S = BC * CD
2: השטח S2 של משולש DEC שווה למחצית מכפלת בסיסו CD בגובהו EF כלומר S2 = CD * EF /2
3: המרובע BEFC הוא מלבן מאחר וזויותיו ישרות - זויות B, BCF הן זויות מלבן ABCD, זוית EFC מבניית עזר, וזוית BEF שווה 90 מעלות משלימה ל- 360 מעלות את שאר זויות המרובע BEFC.
4: BC = EF - נובע מ- 3
5: השטח S2 של משולש DEC שווה : S2 = CD * BC /2 - הצבת 4 ב- 2
6: שטח מלבן ABCD שווה פעמיים שטח משולש DEC -- נובע מ-1 ו-5
מ.ש.ל
הוכחה:
1: השטח S של מלבן ABCD שווה מכפלת גובהו BC בבבסיסו CD כלומר S = BC * CD
2: השטח S2 של משולש DEC שווה למחצית מכפלת בסיסו CD בגובהו EF כלומר S2 = CD * EF /2
3: המרובע BEFC הוא מלבן מאחר וזויותיו ישרות - זויות B, BCF הן זויות מלבן ABCD, זוית EFC מבניית עזר, וזוית BEF שווה 90 מעלות משלימה ל- 360 מעלות את שאר זויות המרובע BEFC.
4: BC = EF - נובע מ- 3
5: השטח S2 של משולש DEC שווה : S2 = CD * BC /2 - הצבת 4 ב- 2
6: שטח מלבן ABCD שווה פעמיים שטח משולש DEC -- נובע מ-1 ו-5
מ.ש.ל



אין תגובות:
הוסף רשומת תגובה