מתוך מבחן מפמ"ר לכיתה ז , 2010
שאלה 25
סכום ארבעה מספרים הוא 45.
אם:
נוסיף 2 למספר הראשון
נחסר 2 מהמספר השני
נכפול ב- 2 את המספר השלישי
נחלק ב- 2 את המספר הרביעי
נקבל ארבעה מספרים שווים זה לזה.
מצאו את כל אחד מהמספרים.
הציגו את דרך החישוב.
פתרון שאלה 25
נסמן ב- x את הערך של את הערך של ארבעת המספרים השווים זה לזה לאחר שינויי הערכים. לכן ערכי המספרים (השווים x ) לפני השינוי הוא:
מספר ראשון (לפני הוספת 2): x-2
מספר שני (לפני חיסור ב- 2): x+2
מספר שלישי: (לפני כפל ב- 2): x/2
מספר רביעי (לפני חילוק ב- 2) : 2x
שאלה 25
סכום ארבעה מספרים הוא 45.
אם:
נוסיף 2 למספר הראשון
נחסר 2 מהמספר השני
נכפול ב- 2 את המספר השלישי
נחלק ב- 2 את המספר הרביעי
נקבל ארבעה מספרים שווים זה לזה.
מצאו את כל אחד מהמספרים.
הציגו את דרך החישוב.
פתרון שאלה 25
נסמן ב- x את הערך של את הערך של ארבעת המספרים השווים זה לזה לאחר שינויי הערכים. לכן ערכי המספרים (השווים x ) לפני השינוי הוא:
מספר ראשון (לפני הוספת 2): x-2
מספר שני (לפני חיסור ב- 2): x+2
מספר שלישי: (לפני כפל ב- 2): x/2
מספר רביעי (לפני חילוק ב- 2) : 2x
סכום ארבעת המספרים הוא 45 לכן:
x - 2 + x + 2 + x/2 + 2x = 45
נפשט ונפתור:
x - 2 + x + 2 + x/2 +2x = 45
4.5x = 45
x = 45 / 4.5 = 10
x = 10
קיבלנו x=10 ,לכן
המספר הראשון: x-2 = 10 -2 = 8
המספר השני:x+2 = 10 + 2 = 12
המספר השלישי: x/2 = 10/2 = 5
המספר הרביעי: 2x = 2ᐧ10 = 20
בדיקת הפתרונות
בדיקת סכום המספרים: 8 + 12 + 5 + 20 = 45
הבדיקה עברה בהצלחה סכום המספרים הוא 45 כפי שנתון בשאלה.
בדיקת פעולות במספרים:
הוספת 2 למספר הראשון: 10 = 2 + 8
חיסור 2 מהמספר השני: 10 = 2 - 12
כפל ב- 2 את המספר השלישי: 10 = 2ᐧ5
חילוק ב- 2 את המספר הרביעי: 10 = 20:2
הבדיקה עברה בהצלחה קיבלנו 4 מספרים שווים (10).
שאלה 26 - חישוב שטח משולש ישר זוית בשני אופנים
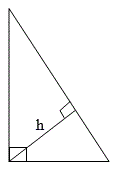
לפניכם משולש ישר זווית.
המספר הראשון: x-2 = 10 -2 = 8
המספר השני:x+2 = 10 + 2 = 12
המספר השלישי: x/2 = 10/2 = 5
המספר הרביעי: 2x = 2ᐧ10 = 20
בדיקת הפתרונות
בדיקת סכום המספרים: 8 + 12 + 5 + 20 = 45
הבדיקה עברה בהצלחה סכום המספרים הוא 45 כפי שנתון בשאלה.
בדיקת פעולות במספרים:
הוספת 2 למספר הראשון: 10 = 2 + 8
חיסור 2 מהמספר השני: 10 = 2 - 12
כפל ב- 2 את המספר השלישי: 10 = 2ᐧ5
חילוק ב- 2 את המספר הרביעי: 10 = 20:2
הבדיקה עברה בהצלחה קיבלנו 4 מספרים שווים (10).
שאלה 26 - חישוב שטח משולש ישר זוית בשני אופנים
לפניכם משולש ישר זווית.
הקטע h הוא גובה ליתר.
נמקו מדוע מכפלת אורכי הניצבים של המשולש הגדול שווה למכפלה של הקטע h באורכו של היתר של המשולש הגדול.
פתרון שאלה 26:
השיטה: נחשב שטח המשולש ישר זוית בשני אופנים: אופן ראשון ע"י מחצית מכפלת הניצבים ואופן שני ע"י שני ע"י מחצית מכפלת היתר והגובה ליתר, ושווה בין התוצאות.
נשרטט את המשולש ישר זוית ונסמן צלעות וקודקודים
נשרטט את המשולש ישר זוית ונסמן צלעות וקודקודים
a ו- b הם ניצבים ו- c הוא היתר.
כידוע שטח משולש שווה מחצית מכפלת צלע בגובה לאותה הצלע.
א. שטח משולש ישר זוית ABC הוא מחצית מכפלת ניצביו
הניצב במשולש ישר זוית הוא צלע אך גם גובה לניצב הסמוך לו לכן שטח משולש ישר זוית ABC הוא: S = aᐧb/2
ב. שטח משולש ישר זוית הוא מחצית מכפלת היתר בגובה ליתר: הקטע h הוא הגובה ליתר c מאחר והוא מאונך לו ויוצא מקודקוד C של המשולש מול היתר c. לכן:
לכן S = cᐧh/2
נשווה בין השטחים שקיבלנו בסעיפים א,ב מאחר והם מתייחסים לאותו משולש ABC ונקבל:
aᐧb/2 = cᐧh/2
aᐧb = cᐧh
קיבלנו שמכפלת אורכי הניצבים של המשולש הגדול (ABC) שווה למכפלה של הקטע h באורכו של היתר של המשולש הגדול. וזה מה שנתבקשנו להוכיח.
כידוע שטח משולש שווה מחצית מכפלת צלע בגובה לאותה הצלע.
א. שטח משולש ישר זוית ABC הוא מחצית מכפלת ניצביו
הניצב במשולש ישר זוית הוא צלע אך גם גובה לניצב הסמוך לו לכן שטח משולש ישר זוית ABC הוא: S = aᐧb/2
ב. שטח משולש ישר זוית הוא מחצית מכפלת היתר בגובה ליתר: הקטע h הוא הגובה ליתר c מאחר והוא מאונך לו ויוצא מקודקוד C של המשולש מול היתר c. לכן:
לכן S = cᐧh/2
נשווה בין השטחים שקיבלנו בסעיפים א,ב מאחר והם מתייחסים לאותו משולש ABC ונקבל:
aᐧb/2 = cᐧh/2
aᐧb = cᐧh
קיבלנו שמכפלת אורכי הניצבים של המשולש הגדול (ABC) שווה למכפלה של הקטע h באורכו של היתר של המשולש הגדול. וזה מה שנתבקשנו להוכיח.


אין תגובות:
הוסף רשומת תגובה