משוואות טריגונומטריות פונקציית סינוס - שיטת פתרון ודוגמאות

הפונקציות הטריגונומטריות הנן מחזוריות וסימטריות (ביחס לצירים אנכיים). לכן בבואנו לפתור משוואה טריגונומטרית עלינו לקחת בחשבון שלעתים יש יותר  מפתרון אחד.

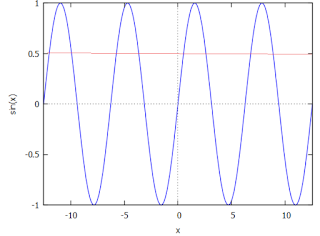גרפי פונקציות: y=sin(x) , y= 0.5  בתחום x = -4pi, 4pi

 

לדוגמה המשוואה הטריגונומטרית: sin(x) = 0.5
לומר כי הפתרון עבור x הוא 30° (קבוצת פתרונות ראשונה) אינו די. אנו יודעים כי sin(x) = sin(180-x) לכן גם הפתרון 150° (קבוצת פתרונות שניה) נכון.

ומה עם זוית 390° ? גם פתרון נכון.

נוכל לסכם כי קיימים אינסוף פתרונות שהם:

x₁ = 30° ± 360°k

x₂ = 150° ± 360°k

k = 0, 1, 2, 3 ....

נוכל להכליל פתרון המשוואה : sin(x) = sin(𝜶) 

x₁ = 𝜶 + 360⁰k

x₂ = 180⁰ - 𝜶 + 360⁰k

k = 0 ,  ±1 ,  ±2 ,  ±3 .... 

כאשר k=0 נקבל את הפתרונות במחזור החיובי הראשון.
כאשר k=1 נקבל את הפתרונות במחזור החיובי השני וכך הלאה.
כאשר k=-1 נקבל את הפתרונות במחזור השלילי הראשון וכך הלאה.

דוגמאות

תרגיל 1 - פתור את המשוואה הטריגונומטרית  :

sin(5x) = 0.8  (= sin 53.13°)

פתרון תרגיל 1

קבוצת פתרונות ראשונה:

5x₁ = 53.13° + 360°k

x₁ = 10.62° + 72°k

קבוצת פתרונות שניה:

5x₂  = (180° - 53.13°)  + 360°k

5x₂ = 126.87°  + 360°k

x₂ = 25.37° + 72°k

תרגיל 2 - פתור את המשוואה הטריגונומטרית  :

sin(3x + 20°) = sin x

פתרון תרגיל 2

קבוצת פתרונות ראשונה:

3x + 20° = x + 360°k

2x = -20° + 360°k

x₁ = -10° + 180°k

x₁ = 170° + 180°k

קבוצת פתרונות שניה:

3x + 20° = 180° - x + 360°k

4x  = 160° + 360°k

x₂ = 40° + 90°k

הערה: אם הפתרון הכללי יוצא שלילי (לדוגמה X1 בדוגמה ב'), אפשר לרשום את הפתרון הכללי כשמתחילים מהפתרון החיובי הראשון וזאת ע"י כך שמוסיפים לפתרון השלילי את המחזור של הפתרון. בדוגמה: ל  10- מעלות מוסיפים 180 מעלות, שזהו המחזור של הפתרון ומקבלים 170 מעלות.

נוכל לסכם גם עבור פונקציות cos, tan, cot:

מחזוריות פונקציות טריגונומטריות: סינוס, קוסינוס, טנגנס, קוטנגנס