בגרות מתמטיקה 4 יחידות קיץ 2019 שאלון ראשון - גיאומטריה אנליטית

מתוך בגרות מתמטיקה 4 יחידות קיץ 2019 שאלון ראשון - שאלה 2

שאלה 2

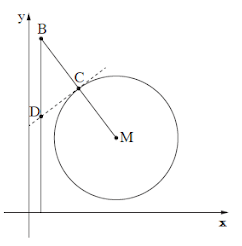
נתון מעגל שמרכזו M(7, 6) . הישר MB חותך את המעגל בנקודה C (ראה איור).

 

מעגל שמרכזו M(7, 6) . הישר MB חותך את המעגל בנקודה C

נתון B(1, 14) ,

MC = BC.

א. מצא את משוואת המעגל.

העבירו משיק בנקודה C.

ב. מצא את משוואת המשיק.

מן הנקודה B הורידו אנך לציר x . המשיק טהאנך נחתכים בנקודה D.

ג. חשב את שטח המשולש BCD.

הנקודה E נמצאת על האנך שהורידו מנקודה B לציר x.

נתון: ME||CD.

ד. מצא את שיעורי הנקודה E.

ה. הראה כי נקודה D היא מרכז המעגל החוסם את משולש BME.

פתרון שאלה 2

א. מציאת משוואת המעגל.
למציאת משוואת המעגל נחוצים הקואורדינטות של מרכזו הנתונות בנקודה M (7,6), ורדיוס המעגל שהוא שווה ל- MC השווה למחצית MB.

נחשב את אורך הקטע MB:
 שיעור הנקודה M הוא (7,6)
שיעור הנקודה B(1,14)

לכן אורך הקטע MB:


לפנינו מעגל שמרכזו בנקודה 7,6 ורדיוסו 5, לכן משוואת המעגל:




ב. משוואת המשיק למעגל בנקודה C

למציאת משוואת המשיק בנקודה C נמצא את שיעורי הנקודה C ואת שיפוע המשיק ועל פיהם נחשב את משוואת המשיק. הנקודה C היא מרכז הקטע MB, ושיפוע המשיק מאונך לשיפוע MB הואיל ומשיק מאונך לרדיוס (MC על קטע MB) בנקודת ההשקה.

ג. שטח המשולש BCD