שאלה
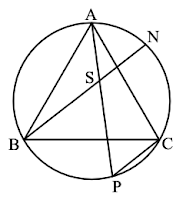
ABC הוא משולש שווה-צלעות החסום במעגל. N ו- P הן נקודות על המעגל.
BN ו- AP נפגשים בנקודה S(ראה ציור).
נתון: PC || BN
הוכח כי:
א. המשולש BSP הוא שווה-צלעות.
ב. המרובע SPCN הוא מקבילית.
ג. AN = PC.
פתרון
א. נוכיח שמשולש BSP שווה צלעות על ידי הוכחה כי 2 מזוויותיו שוות 60 מעלות, ואז גם הזווית השלישית משלימה ל- 180 מעלות שווה גם 60 מעלות ולכן משולש זכל זוויותיו שוות הוא שווה צלעות.
(1) - 600 = SPB⦠ - נשענת על קשת AB של משולש שווה צלעות ABC החסום במעגל.
(2) - 600 = SPC⦠ - נשענת על קשת AC של משולש שווה צלעות ABC החסום במעגל.
(3) - זווית SPC = SPB⦠ - פנימיות מתחלפות PC || BN , חותך SP.
(4) - 600 = BSP⦠ - נובע מ- (2) , (3).
(5) - משולש SPB שווה צלעות מאחר ושתיים מזוויותיו BSP ו- SPB שוות 60 מעלות כל אחת נובע מ - 1, 4.
ב. נוכיח שהמרובע SPCN הוא מקבילית על ידי הוכחת שוויון כל 2 מזויותיו הנגדיות.
(6) זווית APC = זווית BNC = ששים מעלות - הזויות נשענות על קשתות AC, BC של משולש שווה צלעות ABC .
(7) -1200 = NSP⦠ - משלימה את זווית BSP השווה ל 60 מעלות (הוכח ב- 4) ל- 180 מעלות.
(8) 600 = BNC⦠ , נשענת על קשת BC של משולש שווה צלעות ABC החסום במעגל.
(9) - 1200 = NCP⦠ - משלימה את זוויות APC , BNC , NSP ל- 360 מעלות במרובע SPCN (ראה, 6, 7, 8).
(10) - מרובע SPCN מקבילית - מרובע שבו זוויות נגדיות שוות הוא מקבילית. (שיוויון הזוויות נובע מ- 6, 7 ,8, 9).
ג. נוכיח AN = PC.
(11) - PC = SN - צלעות נגדיות במקבילית SPCN שוות.
(12) 600 = BNA⦠ - נשענת על קשת AB של משולש שווה צלעות ABC החסום במעגל.
(13) 600 = ASN⦠. - קודקודית לזווית BSP השווה 60 מעלות (הוכח ב- 4).
(14) - משולש ANS שווה צלעות - נובע מ- 13, 14 - משולש ששתיים מזוויותיו שוות 60 מעלות הוא שווה צלעות.
(15) - AN = SN - נובע מ- 14.
(16) - PC = SN - נובע מ- 15 ו- 11.
מ.ש.ל

אין תגובות:
הוסף רשומת תגובה