שאלה
א. מבין כל המשולשים שהם כאלה, מצא את צלעות המשולש שהיקפו מינימלי.
ב. מה הן תכונות המשולש שאת צלעותיו מצאת בסעיף א׳ ?
פתרון
א. חישוב צלעות המשולש שהיקפו מינימלי
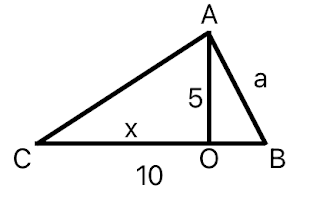
נשרטט את המשולש עם סימולי נקודות וצלעות וגובה:
נסמן CO = x
לפי משפט פיתגורס במשולשים ABO , ACO :
AC² = 5² + x²
AB² = 5² + (10-x)²
היקף p של משולש ABC כפונקציה של x:
sqrt - סימול שורש ריבועי.
p(x) = 10 + sqrt[5² + x²) + sqrt(5² + (10-x)²]
dp/dx = (1/2) ᐧ 2x / sqrt(5² + x²) + (1/2) ᐧ 2(x-10) / sqrt(5² + (10-x)²))
משווים את הנגזרת של p לפי x למציאת עבור אילו ערכי x נקבל ערך קיצון של p:
dp / dx = 0
(1/2) ᐧ 2x / sqrt(5² + x²) + (1/2) ᐧ 2(x-10) / sqrt[5² + (10-x)²)] = 0
ניתן לראות כי המשוואה מקבלת ערך 0 עבור x = 5.
ניתן לראות על פי גרף ההיקף כי כל ערך שנציב מכל x = 5 נקבל היקף גדול יותר.
לכן ההיקף הוא מינימלי עבור x = 5
AC² = 5² + x²
AB² = 5² + (10 - x)²
נציב x = 5:
AC = AB = 5 ᐧ √2
BC = 10 - נתון
BO = BC - OC = BC - x = 10 - 5 = 5
ב. תכונות משולש ABC
הוכחנו בסעיף א כי AC = AB = 5 ᐧ √2 , לכן המשולש הוא שווה שוקיים.
בדיקה מעלה כי:
AB² + AC² = (5 ᐧ √2)² + (5 ᐧ √2)² = 100 = 10² = BC²
כלומר:
AB² + AC² = BC²
מכאן שזווית BAC זווית ישרה על פי משפט פיתגורס ההפוך.
לכן משולש ABC הוא משולש שווה שוקיים וישר זווית.


אין תגובות:
הוסף רשומת תגובה