שאלה
א.הראה כי (f'(x) = 2sin²(x.
ב. (1) האם לפונקציה f(x) יש נקודות קיצון? נמק.
(2) האם לפונקציה f(x) יש נקודות פיתול? נמק.
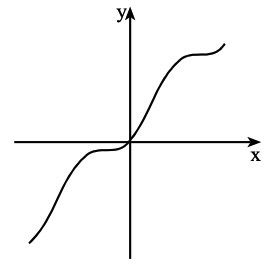
ג. בציור שלפניך מוצג הגרף של הפונקציה g(x) = x + sin²x בתחום π ≤ x ≤ π- .
בתחום הנתון מצא את כל השטח המוגבל על ידי הגרף של g(x) ועל ידי הישר y = x.
ב. (1) האם לפונקציה f(x) יש נקודות קיצון? נמק.
(2) האם לפונקציה f(x) יש נקודות פיתול? נמק.
ג. בציור שלפניך מוצג הגרף של הפונקציה g(x) = x + sin²x בתחום π ≤ x ≤ π- .
בתחום הנתון מצא את כל השטח המוגבל על ידי הגרף של g(x) ועל ידי הישר y = x.
פתרון
א. נגזור את הפונקציה f(x) = x - ½sin(2x)
f(x) = x - ½sin(2x)
f'(x) = 1 - ½ ᐧ 2 ᐧ cos(2x) = 1 - cos(2x) = 1 - ( 1 - 2sin²x) = 2sin²x
f'(x) = 2 ᐧ sin²(x)
ב. (1) האם לפונקציה f(x) יש נקודות קיצון?
לבדיקה האם ל- f(x) יש נקודות קיצון , נבדוק את הנגזרת f'(x) = 2 ᐧ sin²x . בדיקת הנגזרת מעלה כי היא תמיד חיובית או 0, כלומר לעולם לא שלילית. בנקודת קיצון הנגזרת של הפונקציה חייבת לעבור מסימן חיובי לשלילי או להיפך. לכן ל- f(x) אין נקודות קיצון.
(2) האם לפונקציה f(x) יש נקודות פיתול
נבדוק עבור אילו ערכים של x הנגזרת השניה של f(x) מקבלת ערך 0.
f'(x) = 2 ᐧ sin²x
f''(x) = 2ᐧ 2*sin(x) ᐧ cos(x) = 2sin(2x)
הפונקציה sin(2x) מקבלת ערך 0 עבור 2x = 180k או x = 90k עבור k שלם ממינוס אינסוף עד אינסוף.
לכן לפונקציה f(x) יש אינסוף נקודות פיתול, x = 90k עבור k שלם ממינוס אינסוף עד אינסוף.
ג. השטח המוגבל בין g(x) ועל ידי הישר y = x.
השטח המוגבל S בין פונקציה כלשהי f(x) לציר x בתחום כלשהו a, b נתון במשוואה:
x=b
S = ∫ f(x) ᐧ dx
x=a
השטח המוגבל בין 2 פונקציות הוא ההפרש השטחים של שבין הפונקציות לציר x. לכן השטח S המוגבל בין פונקציות f(x) , g(x) הוא בתחום a, b:
S = ∫ f(x) ᐧ dx - ∫ g(x) ᐧ dx = ∫ [f(x) - g(x)] ᐧ dx
לכן השטח המוגבל על ידי הגרף של g(x) = x + sin²x ועל ידי הישר y = x בתחום π ≤ x ≤ π- :
x = π
S = ∫ (x + sin²x - x) ᐧ dx = ∫ sin²x ᐧ dx = [ x/2 - ¼sin(2x)] ᐧ dx =
x = -π
האינטגרל של sin²x חושב לפי מה שהוכח בסעיף א לעיל.
S = π / 2 - (-π)/2 = π

אין תגובות:
הוסף רשומת תגובה