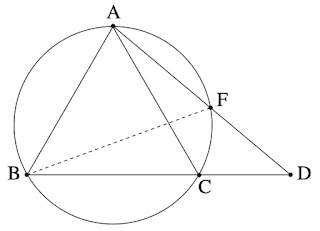
משולש ABC הוא משולש שווה צלעות החסום במעגל שרדיוסו 17 .
הנקודה D נמצאת על המשך הצלע BC , כמתואר בסרטוט.
א. מצאו את אורך הצלע AC .
נתון: CD = 16
ב. מצאו את אורך הקטע AD .
ג. מצאו את גודל הזווית CAD .
הנקודה F היא נקודת החיתוך של הקטע AD עם המעגל.
ד. מצאו את אורך המיתר BF .
ה. (1) מהו גודל הזווית FBC ?
(2) מצאו את שטח המשולש FBD .
נתון: CD = 16
ב. מצאו את אורך הקטע AD .
ג. מצאו את גודל הזווית CAD .
הנקודה F היא נקודת החיתוך של הקטע AD עם המעגל.
ד. מצאו את אורך המיתר BF .
ה. (1) מהו גודל הזווית FBC ?
(2) מצאו את שטח המשולש FBD .
פתרון
א. אורך הצלע AC
נניח מרכז המעגל הנקודה O.
OB = OC = 17 - מרחק נקודה ממרכז המעגל את המעגל שווה לרדיוס.
∠BOC = 120⁰ -
מטעמי סימטריה כל זוית ממרכז המעגל לקודקודי משולש שווה צעות שווה 120 מעלות
לפי משפט הקוסינוסים נחשב את אורך צלע המשולש BC:
BC² = OB² + OC² - 2ᐧOBᐧOCᐧcos(120⁰)
BC² = 17² + 17² - 2ᐧ17ᐧ17ᐧ(-1/2)
BC² = 867
BC = 29.44
מאחר ומשולש ABC הוא שווה צלעות , אורך הצלע AC = BC = 29.44
ב. אורך הקטע AD
נתבונן במשולש ABD :
AB = 29.44 - צלע במשולש שווה צלעות שחושב ב- א.
∠ABD = 60° - זווית במשולש שווה צלעות
BD = BC + CD = 29.44 + 16 = 45.44 - נתון CD , ו - BC היא צלע במשולש שווה צלעות ABC
נמצא את AD על פי משפט הקוסינוסים במשולש ABD.
AD² = AB² + BD² - 2ᐧABᐧBDᐧcos(60⁰) =
AD² = 867 + 2064.8 - 29.44ᐧ45.44 = 1594
AD = 39.92
ג. גודל הזווית CAD
נחשב קודם את גודל הזווית BAD לפי משפט הסינוסים במשולש BAD. אחר-כך נחסר מזוית BAD את זווית BAC השווה 60⁰ . ונקבל את הזווית המבוקשת CAD.
AD / sin(∠ABD) = BD / sin(∠BAD)
39.92 / sin 60⁰ = 45.44 / sin(∠BAD)
sin(∠BAD) = 45.44 ᐧ sin 60⁰ / 39.92
sin(∠BAD) = 0.985
∠BAD = 80.3⁰
∠CAD = ∠BAD - ∠BAC = 80.3⁰ - 60⁰ = 20.3°
ד. אורך המיתר BF
לחישוב אורך המיתר BF נתבונן במשולש ABF.
∠ACB = 60⁰ - זוית במשולש שווה צלעות שווה 60 מעלות
∠AFB =∠ACB = 60⁰ - זויות היקפיות הנשענות על אותה קשת במעגל שוות
∠FBC =∠FAC = 20.3⁰ - זויות היקפיות הנשענות על אותה קשת במעגל שוות
∠ABF = ∠ABC - ∠ABF = 60⁰ - 20.3⁰ = 39.7⁰
∠BAF = 180 - ∠ABF - ∠AFB = 180⁰ - 39.7⁰ - 60⁰ = 80.3°
לפי משפט הסינוסים במשולש ABF :
BF / sin(∠BAF) = AB / sin(∠AFB)
BF / sin(80.3⁰) = 29.44 / sin(∠60⁰)
BF = 29.44 ᐧ sin(80.3⁰) / sin(∠60⁰)
BF = 33.51
ה. (1) גודל הזוית FBC
גודל הזוית FBC חושב בסעיף הקודם.
∠FBC =∠FAC = 20.3⁰ - זויות היקפיות הנשענות על אותה קשת במעגל שוות
(2) שטח המשולש FBD
שטח משולש שווה לnjmh, מכפלת שתי צלעות בסינוס הזוית ביניהן. לכן למציאת שטח משולש FBD נכפיל:
SFBD = FB ᐧ BD ᐧ sin(∠FBC) / 2 =
SFBD = 33.51 ᐧ 45.44 ᐧ sin(20.3⁰) / 2 = 264.1

אין תגובות:
הוסף רשומת תגובה