שאלה
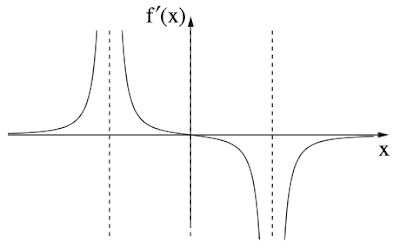
בסרטוט שלפניכם מתואר גרף פונקציית הנגזרת f'(x) , המוגדרת באותו התחום.
גרף פונקציית הנגזרת f'(x) חותך את ציר ה- x בנקודה (0 , 0).
א. מצאו את שיעור ה־ x של נקודת הקיצון של הפונקצייה f(x) , וקבעו את סוגה.
ב. מצאו את תחומי העלייה והירידה של הפונקצייה f(x) .
נתון כי לפונקצייה f(x) יש אסימפטוטה אופקית שמשוואתה היא y = 2.
אחד מן הביטויים III–I שלפניכם מייצג את הפונקצייה f(x) .
ג. קבעו איזה מן הביטויים III–I מייצג את הפונקצייה f(x) . נמקו את קביעתכם.
ד. מצאו את שיעורי נקודות החיתוך של גרף הפונקצייה f(x) עם הצירים.
ה. סרטטו סקיצה של גרף הפונקצייה f(x).
ו. חשבו את השטח המוגבל על ידי גרף פונקציית הנגזרת f'(x) , על ידי ציר ה- x ועל ידי הישר x = 2.
ו. השטח המוגבל על ידי גרף פונקציית הנגזרת f'(x) , על ידי ציר ה- x ועל ידי הישר x = 2
א. מצאו את שיעור ה־ x של נקודת הקיצון של הפונקצייה f(x) , וקבעו את סוגה.
ב. מצאו את תחומי העלייה והירידה של הפונקצייה f(x) .
נתון כי לפונקצייה f(x) יש אסימפטוטה אופקית שמשוואתה היא y = 2.
אחד מן הביטויים III–I שלפניכם מייצג את הפונקצייה f(x) .
ג. קבעו איזה מן הביטויים III–I מייצג את הפונקצייה f(x) . נמקו את קביעתכם.
ד. מצאו את שיעורי נקודות החיתוך של גרף הפונקצייה f(x) עם הצירים.
ה. סרטטו סקיצה של גרף הפונקצייה f(x).
פתרון
א. שיעור ה־ x של נקודת הקיצון של הפונקצייה f(x) , וסוגה
נתון כי גרף פונקציית הנגזרת f'(x) חותך את ציר ה- x בנקודה (0 , 0). בנוסף ניתן לראות כי משמאל לנקודת חיתוך של f'(x) עם ציר x גרף הנגזרת חיובי כלומר f(x) עולה ומימין לנקודת החיתוך גרף הנגזרת שלילי , כלומר f(x) יורדת.
לכן ל- f(x) נקודת מקסימום בנקודה x = 0 .
ב. תחומי העלייה והירידה של הפונקצייה f(x)
בנקודה שבה הנגזרת f'(x) חיובית זה אומר שהשיפוע של f(x) בנקודה זו חיובי כלומר f(x) עולה. בהתאם, בנקודה שבה הנגזרת f'(x) שלילית זה אומר שהשיפוע של f(x) בנקודה זו שלילי כלומר f(x) יורדת.
על פי גרף הפונקציה של f'(x) ניתן לראות כי f'(x) שלילית כאשר x < 0 וחיובית כאשר f'(x) > 0 . לכן הפונקציה f(x) עולה כאשר x>0 ויורדת כאשר x<0, למעט הנקודות בהן f(x) אינה מוגרדת: 3 ± .
ג. איזה מן הביטויים III–I מייצג את הפונקצייה f(x)
הביטוי המתאים לפונקציה f(x) הוא ביטוי III. ביטוי זה מתאר פונקציה שאינה מוגדרת
עבור ערך x = ±3, וזה מתאים לנתוני השאלה.
בנוסף ניתן לראות שכאשר x שואף לאינסוף או מינוס אינסוף ערך הביטוי שואף ל- 2, וזה מתאים לנתון כי לפונקצייה f(x) יש אסימפטוטה אופקית שמשוואתה היא y = 2.
ד. שיעורי נקודות החיתוך של גרף הפונקצייה f(x) עם הצירים
נתונה הפונקציה
f(x) = x² / (x² - 9) + 1
נקודות חיתוך עם ציר y
כאשר x = 0 :
f(0) = 0² / (0² - 9) +1 = 1
נקודת החיתוך : (1 , 0)
נקודות חיתוך עם ציר x
כאשר y = 0
f(x) = 0
f(x) = x² / (x² - 9) + 1 = 0
x² / (x² - 9) = -1
x² = - (x² - 9)
x² = - x² + 9
2x² = 9
x² = 4.5
x = ± 2.121
נקודות החיתוך: (0 , 2.121) , (0 , 2.121-)
ה. סקיצה של f(x)
תחום הגדרה אסימפטוטות :
לפונקציה יש אסימפטוטה אופקית שמשוואתה היא y = 2 - נתון.
הפונקציה אינה מוגדרת עבור ערך x = ±3, מאחר ומכנה יש ביטוי (x^2 - 9). ככל ש- x מתקרב לערכים ±3 , המכנה שואף ל- 0 וזה מגדיל את ערך הפונקציה f(x) = x² / (x² - 9) + 1 . לכן לפונקציה אסימפטוטות עבור x = ±3 .
נקודות חיתוך עם הצירים: (0 , 2.121) , (0 , 2.121-) , (1 , 0)
נקודות קיצון: כפי שעושה בסעיף א לפונקציה נקודת מקסימום עבור x = 0, נחשב את ערך הפונקציה בנקודה זו: f(0) = 1. כלומר לפונקציה נקודות מקסימום (1 , 0).
תחומי עליה / ירידה : הפונקציה עולה עבור x חיובי ויורדת עבור x שלילי , למעט הנקודות x = ±3.
סקיצת הפונקציה : f(x) = x² / (x² - 9) + 1
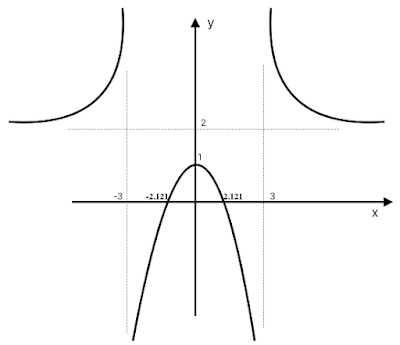 |
סקיצת הפונקציה : f(x) = x² / (x² - 9) + 1 |
ו. השטח המוגבל על ידי גרף פונקציית הנגזרת f'(x) , על ידי ציר ה- x ועל ידי הישר x = 2
השטח המוגבל המבוקש הוא מנקודת חיתוך שמאלית x = 0 ועד x = 2 בין גרף הנגזרת f'(x) לציר x.
2
S = ∫ f'(x)dx = f(2) - f(0) = -4/5 +1 -(0+1) = -4/5
0
השטח המוגבל על ידי גרף פונקציית הנגזרת f'(x) , על ידי ציר ה- x ועל ידי הישר x = 2 הוא 4/5

אין תגובות:
הוסף רשומת תגובה