חקירת פונקציות - תחומי עליה וירידה

 חקירת פונקציות אנו מתבקשים בדרך כלל להציג הסעיפים:
א. תחום הגדרה
ב. נקודות חיתוך עם הצירים
ג. נקודות קיצון
ד. אסימפטוטות
ה. תחומי עלייה וירידה
ו. תאור גרפי

בפרק זה נעסוק בתחומי עליה וירידה של פונקציה.

כפי שראינו, תחום עלייה הינו תחום שבו עם הגדלת x גם f(x) גדל, ותחום ירידה הינו תחום שבו עם הגדלת x הפונקציה f(x) קטנה.
הנגזרת היא השיפוע של המשיק בנקודה. כפי שניתן לראות בציור בתחום עלייה, שיפוע של משיק הוא חיובי ולכן תחום זה מתאפיין ע"י f ‘(x) > 0.
ובתחום ירידה השיפוע הוא שלילי ולכן תחום זה מתאפיין ע"י f ‘(x) <  0.

תחומי עליה וירידה של פונקציה

 

 נקודות קיצון הן גבולות בין תחומי עלייה וירידה. כלומר, משמאל לנקודת מכסימום הפונקציה עולה ומימין הפונקציה יורדת. משמאל לנקודת מינימום הפונקציה יורדת ומימין – עולה. אך נקודות קיצון אינן הנקודות היחידות המשנות את מגמת הפונקציה. גם אסימפטוטות אנכיות יכולות להיות גבול בין תחום עלייה לתחום ירידה, אם כי לא תמיד.


דוגמא
נתונה הפונקציה:
  א.מצא את נקודות המינימום והמקסימום של הפונקציה.
  ב.רשום תחומי עליה וירידה.

פתרון

נקודות קיצון

מציאת נקודות קיצון ע"י השוואת נגזרת ראשונה לאפס.


לפונקציה שתי נקודות קיצון:


נבדוק מהי נקודת מינימום ומהי נקודת מקסימום לפי הנגזרת השניה. אם הנגזרת השניה גדולה מאפס אזי מדובר בנקודת מינימום, ואם הנגזרת השניה קטנה מאפס אזי מדובר בנקודת מקסימום.



הנקודה היא נקודת מינימום מאחר והנגזרת השניה בנקודה x=2 גדולה מאפס.
הנקודה היא נקודת מקסימום מאחר והנגזרת השניה בנקודה x=-1 קטנה מאפס

תחומי עליה וירידה

ניתן למצוא תחומי עליה וירידה בשני אופנים: לפי נקודת מינימום מקסימום, ולפי נגזרת שניה.

לפי נקודת מינימום מקסימום
לפונקציה נקודת מקסימום בנקודה x =-1 ונקודת מינימום בנקודה x = 2.
משמאל לנקודת מכסימום הפונקציה עולה ומימין הפונקציה יורדת. משמאל לנקודת מינימום הפונקציה יורדת ומימין – עולה.
לכן הפונקציה עולה עבור: x < -1 או x>2
הפונקציה יורדת עבור: 

גרף הפונקציה

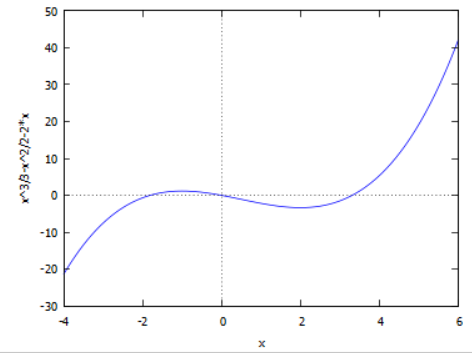גרף פונקציה