האלכסונים בטרפז שווה שוקיים יוצרים עם הבסיסים משולשים שווי-שוקיים

נתון:

 טרפז שווה שוקיים ABCD שבו AB||CD , AD = BC

 

טרפז שווה שוקיים

 

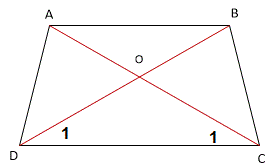
צריך להוכיח: OA = OB , OC = OD

הוכחה:

השיטה: נוכיח חפיפת משולשים BDC,  ACD,
מהחפיפה נובע כי זויות C₁ ו- D₁ שוות ולכן OC = OD (במשולש מול זויות שוות מונחות צלעות שוות)
באותה דרך ניתן גם להוכיח כי OA = OB

ההוכחה:

AD = BC  - נתון (טרפז שווה שוקיים)
AC = BD - בטרפז שווה שוקיים האלכסונים שווים
CD = CD - צלע משותפת

 מכאן נובע :   ACD ≅ △BDC△  לפי משפט חפיפה שלישי צ.צ.צ

 מהחפיפה נובע :   

∠D₁ = ∠C₁

מכאן : OC = OD  - מול זויות שוות במשולש מונחות צלעות שוות (משולש OCD)