הוכח: זוויות נגדיות במעוין שוות זו לזו

נתון:
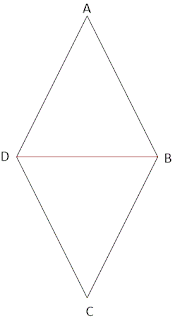
מעוין שקודקודיו ABCD

מעוין

 

צריך להוכיח: זויות נגדיות במעוין שוות זו לזו כלומר:

∢A = ∢C

∢B = ∢D

הוכחה:
שיטה: נוכיח חפיפת משולשים ABD ו- CDB ומהחפיפה נובע שוויון
הזויות: A, C
באותה שיטה מוכיחים שיוויון הזויות B, D.

ההוכחה:

AB = BC - נתון, נובע מהגדרת המעוין (מרובע שצלעותיו שוות)
AD = DC - כנ"ל - נתון
BD - צלע משותפת

מכאן נובע:   ABD ≅ △CDB△   - משפט חפיפה צ.צ.צ.

מהחפיפה נובע:   

∢A = ∢C

באותה דרך מוכיחים שיוויון זויות B, D ע"י חפיפת משולשים ABC, ADC.