משולש ישר זוית חסום בטרפז ישר זוית - טריגונומטריה 4 יח' מתמטיקה

שאלה

 

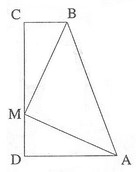
ABCD הוא טרפז ישר זווית (A = ∠D =∠90⁰).

נקודה M נמצאת על הצלע DC (ראה ציור).

נתון: 

 ∠AMB = 90⁰

 AM = MB = k

∠MDA = α

הבע באמצעות k ו-  𝝰 את שטח הטרפז.

פתרון

לצורך פתרון נשרטט את הטרפז ונסמן את הזויות הישרות, זוית 𝝰 ו- k.

נוכיח כי זוית BMC שווה לזוית 𝝰 :

1: במשולש ישר זוית ADM מתקיים:  𝜶 + ∢AMD = 90° - סכום זויות חדות במשולש ישר זוית שווה 90° .

על הישר CD מתקיים: BMC + ∢AMD = 90°⦠ - סכום זויות צמודות על ישר הוא 180°.

2: לכן  180° = BMC + ∢AMD + 90°⦠
מכאן:  BMC = 𝜶⦠ נובע מ- 1 ו- 2.

ע"פ הגדרות סינוס וקוסינוס במשולשים ADM, BMC:

AD = kᐧcos𝝰

MD = kᐧsin𝝰

CM = kᐧcos𝝰

BC = kᐧsin𝝰

 גובה הטרפז CD:

CD = DM + CM =  kᐧcos𝝰 +  kᐧsin𝝰

שטח הטרפז ישר זוית ABCD שנסמנו באות S הוא חצי מכפלת סכום הבסיסים AD ו- BC בגובה CD:

S = ½ ᐧ (AD + BC) ᐧ CD = ½ ᐧ (kᐧcos𝝰 + kᐧsin𝝰)(kᐧcos𝝰 +  kᐧsin𝝰) = ½ ᐧ k² ᐧ (cos𝝰 + sin𝝰)²

S = ½ ᐧ k² ᐧ (cos𝝰 + sin𝝰)²

מ.ש.ל