שאלה 4 - גיאומטריה - ממבחן מפמ"ר לכיתה ט רמה רגילה - תשע"ד
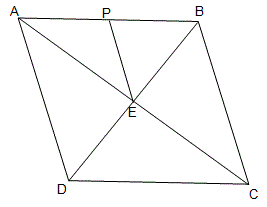
המרובע ABCD מעוין. E נקודת הפגישה של האלכסונים. נתון: ABD משולש שווה צלעות.
EP || BC
הוכיחו:
א. הנקודה P היא אמצע הצלע AB
ב.
ג. המרובע PADE טרפז שווה שוקיים.
פתרון
א. מתבוננים במשולש ABD. משולש ABD שווה צלעות (נתון). E היא אמצע הצלע BD מאחר ואלכסוני המעוין (BD ו- AC) חוצים זה את זה.
PE מקביל ל- BC (נתון) אך גם מקביל ל- AD מאחר והמעוין (ABCD) הוא מקבילית שצלעותיה הנגדיות מקבילות.
מצאנו כי PE מקביל ל- AD ועובר דרך אמצע צלע BD במשולש ABD. מכאן ש- PE הוא קטע אמצעים במשולש ABD ולכן גם חוצה את צלע AB.
הוכחה
1: BE = DE - אלכסוני המעוין (ABCD) חוצים זה את זה
2: EP || BC - נתון
3: BC|| AD - צלעות נגדיות במעוין מקבילות
4. EP || AD - נובע מ- 2,3
5. PE קטע אמצעים במשולש ABD - נובע מ- 1,4 - קטע במשולש היוצא מאמצע צלע אחת (BD) ומקביל לצלע השלישית (AD) חוצה את הצלע השנייה (AB)
6: AP = BP - נובע מ- 5
מ.ש.ל
ב. נדרש להוכיח דמיון משולשים ABD, PBE. נוכיח כי צלעות משולש PBE שוות באורכן למחצית צלעות ABD.
הוכחה:
1: BE = DE - אלכסוני המעוין (ABCD) חוצים זה את זה
2. BE = BD/2 - נובע מ- 1
3. AP = BP - הוכח ב- 6 סעיף קודם (א)
4. BP = AB/2 - נובע מ- 3
5. PE קטע אמצעים במשולש ABD - הוכח ב- 5 סעיף קודם.
6. PE = AD/2 - קטע אמצעים במשולש מחבר אמצעי שתי צלעות במשולש ומקביל לצלע השלישית, ושווה באורכו למחציתה
7. - נובע מ- 2,4,6 - אם בשני משולשים קיים יחס שווה בין שלושת זוגות הצלעות המתאימות אז המשולשים דומים - יחס הדימיון הוא 2.
- נובע מ- 2,4,6 - אם בשני משולשים קיים יחס שווה בין שלושת זוגות הצלעות המתאימות אז המשולשים דומים - יחס הדימיון הוא 2.
מ.ש.ל
ג. נדרש להוכיח כי המרובע PADE טרפז שווה שוקיים. נוכיח שיוויון שוקי הטרפז.
הוכחה
1. AB = BD - משולש ABD שווה צלעות - נתון
2. BE = DE - אלכסוני המעוין (ABCD) חוצים זה את זה
3. AP = BP - הוכח ב- 6 סעיף א
4. AP = DE - נובע מ- 1,2,3 - מחצית גדלים שווים, שווים זה לזה
5. PE קטע אמצעים במשולש ABD - הוכח ב- 5 סעיף א
6. PE||AD - קטע אמצעים במשולש מחבר אמצעי שתי צלעות במשולש ומקביל לצלע השלישית, ושווה באורכו למחציתה
7. מרובע PADE טרפז שווה שוקיים - נובע מ- 4,6
מ.ש.ל
 |
| מעוין שאחד מאלכסוני שווה לצלע |
המרובע ABCD מעוין. E נקודת הפגישה של האלכסונים. נתון: ABD משולש שווה צלעות.
EP || BC
הוכיחו:
א. הנקודה P היא אמצע הצלע AB
ב.
ג. המרובע PADE טרפז שווה שוקיים.
פתרון
א. מתבוננים במשולש ABD. משולש ABD שווה צלעות (נתון). E היא אמצע הצלע BD מאחר ואלכסוני המעוין (BD ו- AC) חוצים זה את זה.
PE מקביל ל- BC (נתון) אך גם מקביל ל- AD מאחר והמעוין (ABCD) הוא מקבילית שצלעותיה הנגדיות מקבילות.
מצאנו כי PE מקביל ל- AD ועובר דרך אמצע צלע BD במשולש ABD. מכאן ש- PE הוא קטע אמצעים במשולש ABD ולכן גם חוצה את צלע AB.
הוכחה
1: BE = DE - אלכסוני המעוין (ABCD) חוצים זה את זה
2: EP || BC - נתון
3: BC|| AD - צלעות נגדיות במעוין מקבילות
4. EP || AD - נובע מ- 2,3
5. PE קטע אמצעים במשולש ABD - נובע מ- 1,4 - קטע במשולש היוצא מאמצע צלע אחת (BD) ומקביל לצלע השלישית (AD) חוצה את הצלע השנייה (AB)
6: AP = BP - נובע מ- 5
מ.ש.ל
ב. נדרש להוכיח דמיון משולשים ABD, PBE. נוכיח כי צלעות משולש PBE שוות באורכן למחצית צלעות ABD.
הוכחה:
1: BE = DE - אלכסוני המעוין (ABCD) חוצים זה את זה
2. BE = BD/2 - נובע מ- 1
3. AP = BP - הוכח ב- 6 סעיף קודם (א)
4. BP = AB/2 - נובע מ- 3
5. PE קטע אמצעים במשולש ABD - הוכח ב- 5 סעיף קודם.
6. PE = AD/2 - קטע אמצעים במשולש מחבר אמצעי שתי צלעות במשולש ומקביל לצלע השלישית, ושווה באורכו למחציתה
7.
מ.ש.ל
ג. נדרש להוכיח כי המרובע PADE טרפז שווה שוקיים. נוכיח שיוויון שוקי הטרפז.
הוכחה
1. AB = BD - משולש ABD שווה צלעות - נתון
2. BE = DE - אלכסוני המעוין (ABCD) חוצים זה את זה
3. AP = BP - הוכח ב- 6 סעיף א
4. AP = DE - נובע מ- 1,2,3 - מחצית גדלים שווים, שווים זה לזה
5. PE קטע אמצעים במשולש ABD - הוכח ב- 5 סעיף א
6. PE||AD - קטע אמצעים במשולש מחבר אמצעי שתי צלעות במשולש ומקביל לצלע השלישית, ושווה באורכו למחציתה
7. מרובע PADE טרפז שווה שוקיים - נובע מ- 4,6
מ.ש.ל

אין תגובות:
הוסף רשומת תגובה