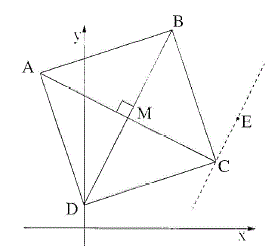
נתון ריבוע ABCD.
אלכסוני הריבוע נפגשים בנקודה (5, 2) M , (ראה ציור) .
שיעורי הקדקוד D הם (1, 0)
א. מצא את שיפוע הישר DM.
ב. מצא את משוואת האלכסון AC.
ג. ישר המקביל לישר DM עובר דרך הנקודה (5, 7) E.
1. מצא את המשוואה של הישר המקביל.
2. הישר שמצאת בתת סעיף ג.1 עובר דרך הקדקוד C.
מצא את השיעורים של הקדקוד C.
ד. מצא את ההיקף של הריבוע ABCD.
פתרון שאלה 2
א.נתון שיעורי נקודה M (2,5) , ושיעורי נקודה D(0,1). שיפוע m של ישר העובר דרך שתי נקודות נתונות
לכן שיפוע m של הישר DM העובר דרך נקודות M (2,5) , D(0,1) הוא:
שיפוע הישר DM הוא 2.
ב.
האלכסון AC של הריבוע מאונך לאלכסון BD של הריבוע מאחר ואלכסוני הריבוע מאונכים זה לזה. קטע DM ששיפועו m=2 הוא חלק מאלכסון BD ולכן גם הוא מאונך לאלכסון AC.מכפלת השיפועים של שני ישרים מאונכים זה לזה היא מינוס אחת לכן שיפוע AC הוא 1/2- .
משוואת הישר בעל שיפוע m העובר דרך נקודה P(x0 , y0) היא: y - y0 = m(x - x0)
לכן משוואה הישר AC ששיפעו 1/2- ועובר דרך נקודה M (2,5) , הוא:
y - 5 = -(1/2)ᐧ(x - 2)
y - 5 = -(1/2)x + 1
y = -(1/2)x + 6
ג.1
משוואת הישר EC העובר דרך נקודה E(7,5) ושיפועו m=2 (כמו שיפוע DM המקביל לו) היא:
משוואת הישר EC העובר דרך נקודה E(7,5) ושיפועו m=2 (כמו שיפוע DM המקביל לו) היא:
y - 5 = 2(x - 7)
y - 5 = 2x - 14
y = 2x -9
ג.2
נקודה C היא נקודת מפגש הישרים AC, EC לכן שיעוריה הוא פתרון משוואות הישרים AC, EC:

שיעורי הנקודה C(6,3)
ד.
למציאת היקף הריבוע ABCD נחשב את אורך צלעו CD ששיעורי קודקודיה C,D ידועים ונכפיל ב- 4
שיעור נקודה D(0,1) ושיערו נקודה C(6,3)
לכן אורך הקטע CD הוא:
נקודה C היא נקודת מפגש הישרים AC, EC לכן שיעוריה הוא פתרון משוואות הישרים AC, EC:
שיעורי הנקודה C(6,3)
ד.
למציאת היקף הריבוע ABCD נחשב את אורך צלעו CD ששיעורי קודקודיה C,D ידועים ונכפיל ב- 4
שיעור נקודה D(0,1) ושיערו נקודה C(6,3)
לכן אורך הקטע CD הוא:
CD = √40 = 2√10
היקף הריבוע הוא 4CD לכן היקפו:
8√10

אין תגובות:
הוסף רשומת תגובה