מעגל חוסם ריבוע - גאומטריה אנליטית - מבגרות מתמטיקה 4 יחידות קיץ 2016

מתוך מבחן בגרות מתמטיקה 4 יחידות קיץ 2016

שאלה 2

 

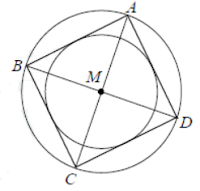
אלכסוני הריבוע ABCD נפגשים בנקודה M. ראה ציור).

 

שיעורי הקדקוד A הם (5, 5).

משוואת האלכסון BD היא y = -(1/3)x.

א. מצא את משוואת האלכסון AC.

ב. מצא את משוואת המעגל החוסם את הריבוע.

ג. חשב את אורך צלע הריבוע.

ד. חשב את אורך הרדיוס של המעגל החסום בריבוע (ראה ציור).

  

פתרון שאלה 2

א. משוואת האלכסון AC

אלכסוני הריבוע מאונכים זה לזה לכן שיפוע אלכסון AC הופכי ונגדי לשיפוע אלכסון BD. שיפוע אלכסון BD הוא 1/3- ולכן שיפוע AC הוא m = 3.
 בנוסף נתון כי AC עובר דרך נקודה A ששיעורה (5, 5).  

משוואת הישר בעל שיפוע m העובר דרך נקודה  P(x₀ , y₀)  היא:  y - y₀ = m(x - x₀)
משוואת AC:
 y - 5 = 3(x - 5)
y - 5 = 3x - 15
y = 3x - 10

ב.משוואת המעגל החוסם את הריבוע

כדי למצוא את משוואת המעגל החוסם את הריבוע נדרש לנו שיעור מרכזו M, ורדיוסו R= MA.
נקודה M היא נקודת חיתוך האלכסונים AC, BD כלומר פתרון המשוואות:
y = -(1/3)x
y = 3x - 10
נפתור:

y = -(1/3)x
y = 3x - 10

-(1/3)x = 3x - 10

-x = 9x - 30

10x = 30

x = 3

y = -1

 שיעור הנקודה M (3, -1)

משוואת המעגל החוסם
רדיוס המעגל R החוסם הוא המרחק בין הנקודה M (3, -1) לנקודה A (5,5)
למשוואת המעגל נדרש לנו ריבוע הרדיוס, נחשב:

R² = MA² = (5 - 3)² + [5 - (-1)²]

R² = 40

R = MA = √(40)

 יש לנו שיעור מרכז המעגל M (3, -1),  וריבוע רדיוס המעגל R² = 40 , לכן משוואת המעגל:

(x - 3)² + (y + 1)² = 40

ג. אורך צלע הריבוע
חישבנו לעיל את מחצית אלכסון הריבוע   MA = √(40), כלומר אורך אלכסון הריבוע:   MA = 2√(40).

לפי משפט פיתגורס נחשב את a אורך צלע הריבוע:

a² + a² = [2√(40)]²

2a² = 4 * 40

a² = 80

a = 4√5

ד. רדיוס המעגל החסום שווה למחצית  צלע הריבוע  5√2 .