נתונה הפונקציה f(x) = (2 - x) / (x - 1)²
א. מצא את תחום ההגדרה של הפונקציה.
ב. מצא את נקודת החיתוך של גרף הפונקציה עם הצירים.
ג. מצא את האסימפטוטות של גרף הפונקציה המאונכות לצירים.
ד. מצא את תחומי העלייה ואת תחומי הירידה של הפונקציה.
ה. סרטט סקיצה של גרף הפונקציה.
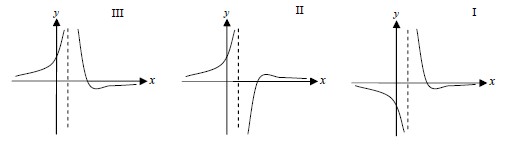
ו. לפניך שלושה גרפים I , II , III.
איזה מן הגרפים מתאר את הנגזרת f'(x) ? נמק.
א. תחום ההגדרה של הפונקציה
נדרוש כי המכנה בפונקציה יהיה שונה מ- 0 משום שחלוקה באפס אינה מוגדרת. לכן תחום ההגדרה עבור x כל מספר פרט ל- 1.
ב. נקודות חיתוך של גרף הפונקציה עם הצירים
נקודת חיתוך עם ציר y כאשר x = 0:
נקודת חיתוך עם ציר y היא: (0,2)
נקודת חיתוך עם ציר x כאשר y=0
נקודת חיתוך עם ציר x היא: (2,0)
נסכם כי נקודות החיתוך עם הצירים הם: (0,2) , (2,0)
אסימפטוטה מאונכת לציר x
אסימפטוטה מאונכת לציר x בנקודה כלשהי נניח x = a תתקבל אם נשאיף את x ל- a, אזי הפונקציה f(x) תשאף לאינסוף. ניתן לראות שכאשר (x שואף ל- 1) x --> 1 הפונקציה f(x) שואפת לאינסוף. לכן יש אסימפטוטה מאונכת לציר x בנקודה x = 1, או המילים אחרות הישר x = 1 הוא אסימפטוטה.
אסימפטוטה מאונכת לציר y
אסימפטוטה מאונכת לציר y בנקודה כלשהי נניח y= b תתקבל אם נשאיף את x לאינסוף, אזי הפונקציה f(x) תשאף ל- b.
אם נשאיף את x לאינסוף אזי f(x) ישאף לאפס מאחר ובמונה המעלה של x היא 1 ובמכנה המעלה של x היא 2.
לכן הישר y = 0 הוא אסימפטוטה לפונקציה f(x) מאונכת לציר y.
אין תגובות:
הוסף רשומת תגובה