נתונה הפונקציה f(x) = -3ᐧexᐧ(2ᐧex - 4) .
א. מצא את תחום ההגדרה של f(x).
ב. מצא את שיעורי החיתוך של גרף הפונקציה f(x) עם הצירים.
ג. מצא את שיעורי נקודות הקיצון של הפונקציה f(x), וקבע את סוגה.
ד. סרטט סקיצה של גרף הפונקציה f(x).
ה. נתונה הפונקציה g(x) = -(1/2)ᐧf(x).
(1) כתוב מה הם שיעורי נקודת הקיצון של הפונקציה g(x) , וקבע את סוגה.
(2) סרטט סקיצה של גרף הפונקציה g(x).
פתרון שאלה 4
א. תחום ההגדרה של הפונקציה f(x) = -3ᐧexᐧ(2ᐧex - 4).
ניתן לראות כי אין הגבלה לערך ש- x יכול לקבל מאחר ואינו בשורש, מכנה .
ב. נקודות חיתוך הפונקציה f(x) עם הצירים
נקודות חיתוך עם ציר y כאשר x =0.
f(0) = -3ᐧe0ᐧ(2ᐧe0 - 4) = -3ᐧ(2 - 4) = 6
נקודת חיתוך עם ציר y היא: (6 , 0).
נקודות חיתוך עם ציר y כאשר f(x) =0.
f(x) = -3ᐧexᐧ(2ᐧex - 4) = 0
exᐧ(2ᐧex - 4) =0
אפשרות ראשונה:
ex = 0
אין x המקיים משוואה זו.
אפשרות שניה:
2ᐧex - 4 = 0
2ᐧex = 4
ex = 2
x = ln2
נקודת חיתוך עם ציר x היא: (0 , ln2).
נקודות החיתוך של הפונקציה f(x) עם הצירים: (6 , 0) , (0 , ln2) .
ג. נקודות קיצון של הפונקציה f(x) וסוגיהן
ד. סקיצה של גרף הפונקציה f(x)
ד. סקיצה של גרף הפונקציה f(x)
נרכז את הנתונים הידועים לנו על הפונקציה f(x).
f(x) = -3ᐧex(2ᐧex - 4)
נקודות חיתוך עם הצירים: (6 , 0) , (0 , ln2)
נקודת מקסימום: (6 , 0) .
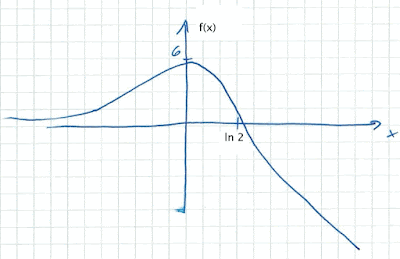
סקיצה:
 |
| סקיצה של גרף הפונקציה f(x) |
ניתן לראות שככל ש- x שואף ל- ∞- אז f(x) שואף ל- 0 .
לכן קיימת אסימפטוטה לפונקציה אופקית y = 0.
ככל ש- x שואף ל- ∞+ אז f(x) שואף ל- ∞- , לפיכך הסקיצה שורטטה בהתאם.
סעיף ה - פונקציה g(x): מציאת נקודות קיצון ושרטוט סקיצה
אין תגובות:
הוסף רשומת תגובה