שאלה מספר 1
אורך הקטע AB הוא 4.
נתון: הנקודה A נמצאת על ציר ה- y , והנקודה B נמצאת על ציר ה- x (ראה ציור).
הנקודה M היא אמצע הקטע AB.
א. מצא את המשוואה של המקום הגיאומטרי של כל הנקודות M שנבנו כך, וזהה את המקום הגאומטרי הזה.
נתון: הנקודה L נמצאת על הקטע AB כך ש- AL/LB = t . כאשר t>0 הוא פרמטר.
ב. הבע באמצעות t את המשוואה של המקום הגאומטרי של כל הנקודות L שנבנו כך, וזהה את המקום הגאומטרי הזה.
ג. בעבור איזה ערך של t המקום הגאומטרי שמצאת בסעיף ב מתלכד עם המקום הגאומטרי שמצאת בסעיף א? נמק.
ד. האם קיים t>0 שבעבורו המקום הגאומטרי שנמצאת בסעיף ב חותך את ציר ה- x בנקודה (0, 5)? נמק.
פתרון שאלה מספר 1
אורך הקטע AB הוא 4.
נתון: הנקודה A נמצאת על ציר ה- y, והנקודה B נמצאת על ציר ה- x (ראה ציור).
נתון: הנקודה A נמצאת על ציר ה- y, והנקודה B נמצאת על ציר ה- x (ראה ציור).
 |
| הנקודה A נמצאת על ציר ה- y, והנקודה B נמצאת על ציר ה- x |
הנקודה M היא אמצע הקטע AB.
סעיף א - מצא את המשוואה של המקום הגיאומטרי של כל הנקודות M שנבנו כך, וזהה את המקום הגיאומטרי הזה.
פתרון סעיף א - נשרטט את הנקודה M על אמצע הקטע AB ואת שיעוריה x,y .
אם שיעור הנקודה M הוא x,y , אזי שיעור הנקודה B הוא 2x, ושיעור הנקודה A הוא 2y מאחר ו- M היא אמצע הקטע AB.
אורך הקטע AB הוא אפוא:
סעיף א - מצא את המשוואה של המקום הגיאומטרי של כל הנקודות M שנבנו כך, וזהה את המקום הגיאומטרי הזה.
פתרון סעיף א - נשרטט את הנקודה M על אמצע הקטע AB ואת שיעוריה x,y .
אם שיעור הנקודה M הוא x,y , אזי שיעור הנקודה B הוא 2x, ושיעור הנקודה A הוא 2y מאחר ו- M היא אמצע הקטע AB.
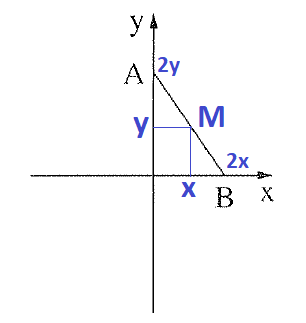 |
| הנקודה M על אמצע הקטע AB |
אורך הקטע AB הוא אפוא:
AB² = 4² = (2x)² + (2y)²
4x² + 4y² = 16
x² + y² = 4
x, y הם שיעורי הנקודה M. מכאן, המקום הגיאומטרי של הנקודה M הוא מעגל שמרכזו ראשית הצירים ורדיוסו 2.
המשך סעיפים ב-ד
נתון: הנקודה L נמצאת על הקטה AB כך ש: t = AL / BL .
t >0 הוא פרמטר.
ב. הבע באמצעות t את המשוואה של המקום הגיאומטרי של כל הנקודות L שנבנו כך, וזהה את המקום הגיאומטרי הזה.

חיןחןחן
השבמחק