מבגרות מתמטיקה 4 יחידות קיץ 2023 - שאלון 035481
שאלה מספר 4
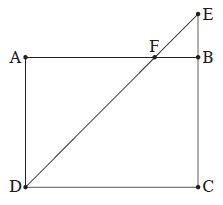
המרובע ABCD הוא מלבן.
הנקודה E נמצאת על המשך הצלע CB , כמתואר בסרטוט שלפניכם.
הקטע DE חותך את הצלע AB בנקודה F.
א. הוכיחו: BFE ≌ △AFD△
נתון כי שטח המשולש AFD גדול פי 9 משטח המשולש BFE.
ב. מצאו את היחס AF / FB.
נתון: EB = 8 .
שטח המלבן ABCD הוא 768 .
ג. (1) מצאו את אורך הצלע CB.
(2 ) מצאו את אורך רדיוס המעגל החוסם את המשולש DCE.
פתרון שאלה מספר 4
א. הוכחת דמיון משולשים BFE , AFD
נוכיח דמיון משולשים AFD, BFE באמצעות שיוויון 2 זוויות.
זווית EFB = זווית AFD - זוויות קדקודיות
A = ⦟ EBF = 90⁰⦟ - הזווית A היא זווית במלבן ולכן ישרה. זווית EBF צמודה לזווית במלבן ולכן ישרה גם היא.
מכאן: BFE ≌ △AFD△ - אם בשני משולשים שוות בהתאמה שתי זוויות המשולשים דומים.
ב. מציאת היחס AF / FB.
יחס השטחים במשולשים דומים הוא ריבוע יחס הצלעות התאימות. לכן אם שטח המשולש AFD גדול פי 9 משטח המשולש BFE, אזי יחס הצלעות המתאימות AF / FB שווה 3.
ג (1). אורך הצלע BC
נתונים לנו כי שטח המלבן ABCD הוא 768, ו- EB = 8.
יחס הדמיון בין המשולשים AFD , BFE הוא 3 (הוכח בסעיף קודם).
BC = AD - לפי ש- ABCD מלבן , צלעות נגדיות במלבן שוות.
AD / BE = 3 = AD /8 - יחס הדמיון בין המשולשים AFD , BFE הוא 3 ונתון BE = 8.
לכן : AD = 24 = BC
BC = 24
(2) . מצאו את אורך רדיוס המעגל החוסם את המשולש DCE
נוכיח כי המשולש DCE הוא שווה שוקיים ישר זווית ולכן הניצבים שלו CD, CE הם גם רדיוסים המעגל החוסם.
ABCD שטח המלבן = 768 = CD * BC = 24 * CD - שטח מלבן ABCD שווה 768 , למכפלת צלעותיו CD , BC.
לכן : CD = 768 / 34 = 32
אך : CE = BC + BE = 24 + 8 = 32
לכן CD = CE = 32 , וכן משולש ABCD הוא שווה שוקיים ישר זווית שבו CD, CE ניצבים שווים, וכן רדיוסים המעגל החוסם משולש ECD.
לכן אורך רדיוס המעגל החוסם משולש ECD שווה 32.

אין תגובות:
הוסף רשומת תגובה