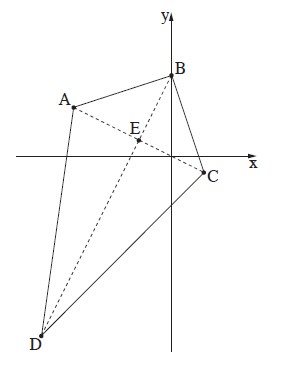
BA = BC , DA = DC .
אלכסוני הדלתון נפגשים בנקודה E .
נתון: ( A(-6, 3) , C(2, -1
הקודקוד B נמצא על ציר ה־ y , והקודקוד D נמצא ברביע השלישי.
א. (1) מצאו את משוואת האלכסון BD.
( 2) מצאו את שיעורי הקודקוד B.
נתון: שטח הדלתון ABCD הוא 80 .
ב . מצאו את האורך של האלכסון BD . השאירו שורש בתשובתכם.
ג. מצאו את שיעורי הקודקוד D.
ד . מצאו את משוואת המעגל שמרכזו בנקודה A והישר BD משיק לו. הסבירו.
פתרון שאלה מספר 4
א (1) . משוואת האלכסון BD
האלכסון BD מאונך לאלכסון AC (אלכסוני הדלתון מאונכים זה לזה) שאפשר למצוא את שיפועו מאחר ונתונים לנו שיעורי הנקודות A, C. ןלכן נמצא גם את שיפוע האלכסון BD המאונך לו.
בנוסף האלכסון BD עובר דרך נקודה E, שהיא אמצע הנקודות A, C הנתונות לנו. לכן נוכל למצוא את שיעור הנקודה E.
לפיכך נוכל מצוא את משוואת האלכסון BD על פי שיפוע (מאונך לאלכסון AC) ועל פי נקודה דרכה הוא עובר, E.
נתון: ( A(-6, 3) , C(2, -1
לכן שיפוע AC:
שיפוע AC = (3+1) / (-6-2) = -4/8 = -1/2
שיפוע BD המאנך ל- AC הוא מינוס ההופכי שלו:
שיפוע BD = -1 / (שיפוע AC) = 2
נקודה E נמצאת באמצע הנקודות A ,C, לכן שיעור הנקודה E:
x = (-6 + 2) / 2 = -2
y = [3 + (-1)] / 2 = 1
משוואת BD תחושב על פי חישבו משוואת ישר על פי שיפועו ונקודה דרכה הוא עובר:
y - 1 = 2( x + 2)
y - 1 = 2x + 4
משוואת הישר העובר דרך הנקודות B, D הוא:
y = 2x + 5
א (2) שיעור הקדקוד B.
B היא נקודת החיתוך של הישר y = 2x + 5 ( חישבנו בסעיף הקודם א (1) ) עם ציר y. נציב משוואת הישר x = 0 ונקבל y = 5 .
שיעור הנקודה B הוא : ( 5 , 0).
ב. אורך האלכסון BD.
נתון שטח הדלתון ABCD שווה 80. ניתן למצוא את אורך האלכסון AC על פי מרחק בין שתי הנקודות A, C.
מציבים בשטח הדלתון 80 = S שהוא מחצית מכפלת אלכסוניו (המאונכים זה לזה) :
S = (AC ᐧ BD) / 2 = 80
AC ידוע ומחלצים את BD.
נתון: ( A(-6, 3) , C(2, -1
לכן :
AC² = (-6-2)² + [3-(-1)]² = 80
AC = 4√5
נציב את AC במשוואת שטח הדלתון:
(AC ᐧ BD) / 2 =(4√5 ᐧ BD) / 2= 80
BD = 8√5
ג. שיעור הקדקוד D
נקודה D נמצאת במרחק BD = 8√5 מנקודה B (0 ,5) וגם על הישר y = 2x + 5 .
נציב ונפתור שתי משוואות בשני נעלמים:
y = 2x + 5
(x - 0)² + (y - 5)² = (8√5)ᐧ2 = 320
לשתי המשוואות 2 פתרונות אולם רק אחד ל - x, y ברביע השלישי והוא:
x = -8 , y = -11 . לכן שיעור הנקודה D הוא ( 11- , 8-).
ד. משוואת המעגל שמרכזו בנקודה A והישר BD משיק לו
תנאי השקת ישר למעגל הוא שרדיוס המעגל מאונך למשיק בנקודת ההשקה. מעגל שמרכזו בנקודה A משיק לישר BD בנקודה E מאחר ו- AE מאונך ל BD (אלכסונים בדלתון מאונכים זה לזה). לכן E היא נקודת ההשקה ו- AE הוא רדיוס המעגל בנקודה A ש- BD משיק לו.
מציאת AE (רדיוס המעגל) :
AE שווה למחצית AC כי האלכסון הראשי בדלתון (BD) חוצה את האלכסון המשני AC.
AE = AC / 2 = (4√5) / 2 = 2√5
שיעור הנקודה A נתון לנו A(-6, 3)לכן משוואת המעגל שמרכזו בנקודה A(-6, 3)ורדיוסו 2√5 הוא:
(x + 6)² + (y - 3)² = (2√5)²
(x + 6)² + (y - 3)² =20

אין תגובות:
הוסף רשומת תגובה