מבגרות מתמטיקה 4 יחידות קיץ 2023 - שאלון 035481
שאלה מספר 5
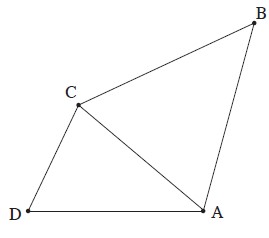
בסרטוט שלפניכם מתוארים שני משולשים:
משולש ADC שכל זוויותיו חדות, ומשולש שווה שוקיים ABC שבו BC=BA .
נתון: שטח המשולש ABC הוא 114 ,
ABC = 50⁰⦛.
א. מצאו את אורך הצלע AB.
ב. מצאו את אורך הצלע AC.
נתון: רדיוס המעגל החוסם את המשולש ADC הוא 8 .
ג. מצאו את גודל הזווית ADC.
נתון: AD=15 .
ד. מצאו את גודל הזווית CAD .
ה. מצאו את אורך BD .
פתרון שאלה מספר 5
א. אורך הצלע AB
שטח משולש שווה למחצית מכפלת שתי צלעות בסינוס הזווית ביניהן. ניתן בנקל להוכיח זאת.
נסמן אורך כל אחת מהשוקיים השוות במשולש ABC באות a.
כלומר BC = BA = a .
לכן שטח משולש ABC הוא :
BC * BA * sin(∢ABC) / 2 = a * a * sin(50⁰) / 2 = 114
a * a = 148.8
a = 17.25
אורך הצלע AB הוא 17.25 .
ב. אורך הצלע AC
ניתן לחשב את גודל זויות BAC ו- BCA מאחר והן מןנחות מול צלעות שוות BA = BC , וגודל זווית B נתון לנו 50 מעלות :
∢BAC = ∢BCA = (180⁰ - 50⁰) / 2 = 65⁰
לפיכך על פי משפט הסינוסים במשולש BAC מתקיים:
AC / sin(∢B) = AB / sin(∢BCA)
AC / sin(50⁰) = 17.25 / sin(65⁰)
AC = 17.25 * sin(50⁰) / sin(65⁰) = 14.58
אורך הצלע AC הוא 14.58.
ג. מציאת גודל הזווית ADC
נתבונן במשולש ADC
רדיוס המעגל החוסם את משולש ADC הוא R = 8 - נתון מסעיף ג בשאלה.
AC = 14.58 - חישבנו בסעיף ב.
על פי משפט הסינוסים צלע במשולש לחלק בסינוס הזווית שמולה שווה לפעמיים רדיוס המעגל החוסם את המשולש.
כלומר במשולש ADC מתקיים:
AC / sin(∢D) = 2R
14.58 / sin(∢D) = 2 * 8
sin(∢D) = 14.58 / 16
∢D = 65.68⁰
ד. גודל הזווית CAD
במשולש ADC ידועה לנו גודל הזווית ADC (זווית D) :
∢D = 65.68⁰
נמצא את זווית ACD במשולש ADC על פי אורך הצלע AD = 15 (נתון) מול זווית ACD, ורדיוס המעגל החוסם את משולש ADC הנתון לנו R = 8 (נתון).
על פי משפט הסינוסים במשולש ADC
AD / sin(∢ACD) = 2R
15 / sin(∢ACD) = 16
sin(∢ACD) = 15 / 16
∢ACD = 44.68⁰
ה. אורך BD
נמצא את BD לפי משפט הקוסינוסים במשולש ABD.
נשתמש בנתונים ומה שחישבנו בסעיפים קודמים:
AD = 15 - נתון
AB = 17.85 - מצאנו בסעיף א.
∢BAD = ∢BAC+ ∢DAC
∢BAD = 65⁰ + 44.68⁰
∢BAD = 109.68⁰
לפי משפט הקוסינוסים במשולש BAD:
BD² = AD² + AB² - 2*AB*AD*cos(∢BAD)
BD² = 15² + 17.25² - 2*15*17.25*cos(∢109.68⁰)
BD = 26.39

אין תגובות:
הוסף רשומת תגובה