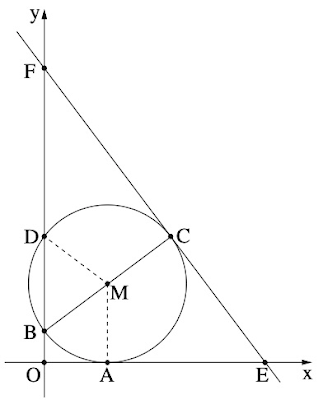
מעגל שמרכזו M משיק לציר ה־ x בנקודה A . הנקודה O היא ראשית הצירים.
המעגל חותך את ציר ה־ y בנקודות B ו־ D , כמתואר בסרטוט.
נתון : A (8, 0) , D (0, 16) .
א. (1) מצאו את שיעורי הנקודה M .
(2) מצאו את משוואת המעגל.
(3) מצאו את שיעורי הנקודה B .
הנקודה C נמצאת על המעגל כך ש־ BC הוא קוטר.
דרך הנקודה C העבירו משיק למעגל, החותך את ציר ה־ x בנקודה E , ואת ציר ה־ y בנקודה F .
ב. מצאו את משוואת המשיק.
ג. האם הנקודה C היא מרכז המעגל החוסם את המשולש EFO ? נמקו את תשובתכם.
פתרון
א. (1) שיעור הנקודה M
המעגל משיק לציר ה־ x בנקודה A . לכן הרדיוס MA מאונך לציר x מאחר ורדיוס לנקודת ההשקה מאונך למשיק .
לכן שיעור ה- x של נקודה M שווה לשיעור ה- x של נקודה A :
xM = 8.
AM = DM - רדיוסים של מעגל M.
נרשום משוואות מרחק בין הנקודות AM = DM ונציב xM = 8.
(0 - 8)² + (16 - yM)² = (8 - 8)² + (0 - yM)²
64 + 256 - 32yM + yM² = yM²
32yM = 320
yM =10
שיעור הנקודה M מרכז המעגל הוא (10, 8)
(2) משוואת המעגל
יש לנו את שיעור הנקודה M נמצא את רדיוס המעגל על ידי חישוב מרחק נקודת מרכז המעגל
M(8, 10), מנקודה על המעגל A (8, 0). המרחק הוא 10 ולכן רדיוס המעגל הוא 10.
משוואת המעגל שמרכזו בנקודה M(8, 10) :
(x - 8)² + (y - 10)² = 10²
(3) שיעור הנקודה B
הנקודה B היא נקודת חיתוך המעגל עם ציר y כלומר כאשר x = 0:
(0 - 8)² + (yB - 10)² = 0
64 + yB² - 20yB + 100 = 100
yB² - 20yB + 64 = 0
(yB - 4)(yB - 16) = 0
הפתרון המתאים לנקודה B הוא yB = 4, מאחר ו- 16 הוא שיעור y הנקודה D.
לכן B(0, 4).
ב. משוואת המשיק
למציאת משוואת המשיק נמצא קודם את משוואת BC המאונך למשיק ויש נקודה משותפת C עם המשיק.
הנקודות B(0, 4), M(8, 10) שמצאנו לעיל , על הישר BC ולכן נוכל למצוא את משוואת BC:
B(0, 4) היא נקודת חיתוך עם ציר y, לכן משוואת BC היא מהצורה:
y = aᐧx + 4
כאשר a הוא שיפוע BC:
a = (10 - 4) / (8 - 0) = 6 / 8 = 3 / 4
y = (3 / 4)x + 4
שיעור נקודה C
נקודה M(8, 10) (מרכז המעגל) היא נקודת האמצע של הנקודות B(0, 4), C על המעגל כאשר BC מקווה קוטר (נתון).
לכן:
8 = (0 + xC) / 2
10 = (4 + yC) /2
xC = 16
yC = 16
משוואת המשיק:
המשיק מאונך ל- BC ששיפועו 4 /3 , ועובר דרך נקודה C(16, 16). לכן משוואת המשיק:
y - 16 = -(4/3)(x - 16)
y = -(4/3)x + 16 + 4ᐧ16/3 = -(4/3)x + 3ᐧ16 / 3 + 4 * 16 /7 =
= -(4/3)x + 7ᐧ16 / 3 = -(4/3)x + 3ᐧ16 / 3 + 4 ᐧ 16 /7 = -(4/3)x + 112 / 3
ג. האם הנקודה C היא מרכז המעגל החוסם את המשולש EFO
משולש EFO הוא משולש ישר זווית. נבדוק האם CO הוא תיכון ליתר EF. אם כן אזי התיכון CO שווה למחצית היתר EF , ולכן EC = FC = CO ולכן נקודה C היא מרכז המעגל החוסם את משולש EFO.
משוואת המשיק:
y = -(4/3)x + 112 / 3
שיעור הנקודה C(16, 16).
שיעור נקודה F, נקודת חיתוך המשיק עם ציר y, נציב x = 0 נקבל y = 112 / 3 ו- 16 (שיעור ה- y של נקודה C) אינו שווה למחצית ערך זה.
לכן נקודה C אינה מרכז הקטע EF . ולכן נקודה C אינה מרכז המעגל החוסם את משולש EFO.

אין תגובות:
הוסף רשומת תגובה