נתון
מעגל O (a , b) שרדיוסו r, ונקודה A (c, d) מחוץ למעגל.
מנקודה Aיוצאים שני משיקים למעגל O בנקודות B, C.
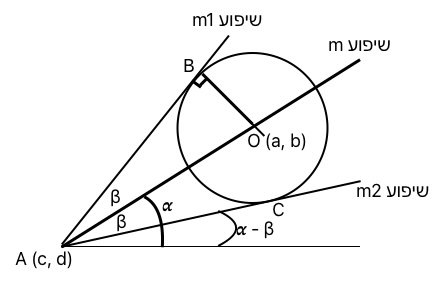 |
| שני משיקים למעגל היוצאים מנקודה אחת |
נדרש
מצא את משוואות המשיקים AC , AB.
פתרון
נסמן :
L = AO - הישר מנקודה A למרכז המעגל O.
𝜶 - הזוית שיוצר AO עם ציר x.
β - הזוית הנוצרת בין כל אחד מהמשיקים AB, AC לקטע AO.
m - שיפוע ישר AO
m1 - שיפוע הישר AB
m2 - שיפוע הישר
השיטה:
נחשב את שיפוע הקטע AO , ואת זוית β בין כל אחד מהמשיקים לקטע AO. נחשב את שיפועי המשיקים על פי שיפוע AO (זוית 𝜶) וזוית β. נחשב את משוואות המשיקים על פי שיפועם ונקודה A ממנה הם יוצאים.
מציאת m - שיפוע AO
הישר AO מחבר בין מרכז המעגל O(a , b) , לבין הנקודת A(c, d) . לכן השיפוע שווה:
m = (b - d) / (a - c)
𝜶 היא הזוית שיוצר AO עם ציר x , לכן:
tan(𝜶) = m
מציאת L = AO
L הוא המרחק בין נקודה O (a , b) ונקודה A (c, d) , לכן:
L^2 = (a - c)² + (b - d)²
L = sqrt((a - c)² + (b - d)²)
מציאת זוית β
sin(β) = OB / OA = r / L
נחשב את טנגנס:
tan(β) = sin(β) / sqrt(1 - (sin(β))²) = ( r / L) / sqrt(1 - (r/L)²)
= ( r / L) / sqrt(1 - r²/L² ) = ( r / L) / (sqrt(L² - r²) / L)
tan(β) = r / sqrt(L² - r²) = n
מציאת שיפועי המשיקים:
m1 = tan(𝜶 + β)
m2 = tan(𝜶 - β)
לחישוב m1 , m2 נשתמש בזהות:
m1 = tan(𝜶 + β) = (tan(𝜶) + tan(β)) / (1 - tan(𝜶)ᐧtan(β))
m2 = tan(𝜶 - β) = (tan(𝜶) - tan(β)) / (1 + tan(𝜶)ᐧtan(β))
נציב
tan(𝜶) = m
tan(β) = n
נקבל:
m1 = (m + n) / (1 - mᐧn)
m2 = (m ᐧ n) / (1 + mᐧn)
מציאת משוואות המשיקים:
באופן דומה משוואת המשיק השני:
y = m2ᐧx + n2
דוגמא:
נתון מעגל O (5 , 5) שרדיוסו 1, ונקודה A (1, 1) מחוץ למעגל
חשב את משוואות המשיקים מנקודה A למעגל O.
פתרון
נרשום את הנתונים ונציב בנוסחאות לעיל.
a = 5
b = 5
r = 1
c = 1
d = 1
m = (b - d) / (a - c) = (5 - 1) / (5 - 1) = 1
L² = (a - c)² + (b - d)² = (5 -1)² + (5 - 1)² = 32
n = r / sqrt(L² - r² ) = 1 /sqrt(32 - 1) = 0.1796
שיפועי המשיקים:
m1 = (m + n) / (1 - m*n) = (1 + 0.1796) / (1 - 1ᐧ0.1796) = 1.4379
m2 = (m - n) / (1 + m*n) = (1 - 0.1796) / (1 + 1ᐧ0.1796) = 0.6955
נקודות חיתוך המשיקים עם ציר y:
n1 = d - m1ᐧc = 1 - 1ᐧ1.4379 = -0.4379
n2 = d - m2ᐧc = 1 - 0.6955*1 = 0.3045
משוואות המשיקים:
y = 1.4379 ᐧ x - -0.4379
y = 0.6955 ᐧ x + 0.3045
להלן סקיצה של המעגל והמשיקים:


אין תגובות:
הוסף רשומת תגובה