הוכחת המשפט : זווית בין משיק למיתר במעגל שווה לזווית ההיקפית הנשענת על המיתר

נתון

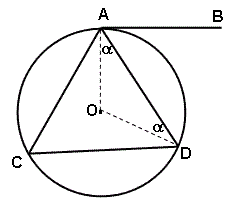
AB משיק למגל O בנקודה A, ו AD מיתר.

צריך להוכיח

BAD⦠ו = C ⦠

הוכחה

1. נעביר רדיוסים OA ו- OD.

2. 𝜶 ו =  ODA⦠ו = OAD ⦠ - מול צלעות שוות זוויות שוות (לפי 1) + סימון.

3. 𝜶180° - 2𝜶ו= AOD ⦠ - סכום זוויות במשולש AOD שווה 180° (לפי 2)

4.   𝜶90° - 𝜶ו=C ⦠ - זווית היקפית שווה למחצית הזווית המרכזית הנשענת על אותה קשת (לפי 3).

5. AB משיק  - נתון.

6.   𝜶90°ו=OAB ⦠ - זווית בין משיק לרדיוס שווה 90° (לפי 1,5).

7.   𝜶90° - 𝜶ו = BAD ⦠ -  חישוב (לפי 2, 6).

8. BAD⦠ו = C ⦠ - כלל המעבר (לפי 4,7).

מ.ש.ל.