מתי מתוק: שטח טרפז וטריגונומטריה - מבגרות מתמטיקה 3 יחידות

שאלה

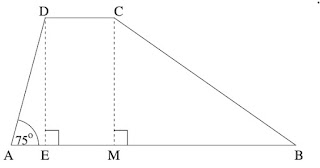
בסרטוט שלפניכם מתואר טרפז ABCD (AB||CD) .

DE ו־ CM הם גבהים בטרפז.

נתון: AE = 4 , CB = 26 ,

75⁰ = DAE⦩

א. מצאו את אורך הגובה DE .

ב. מצאו את גודל הזווית CBM .

נתון CD = 8 .

ג. מצאו את אורך הבסיס AB .

ד. חשבו את שטח הטרפז ABCD .

פתרון

א. אורך הגובה DE .

נתבונן במשולש ADE:

tan(⦨DAE) = DE / AE

DE = tan⦨DAE ᐧᐧ AE = tan75⁰ * 4 = 14.928

DE = 14.928

ב. גודל הזווית CBM .

נתבונן במשולש CBM:

המשולש הוא ישר זווית מאחר ו- CM הוא גובה ומאונך לבסיס AB.

הצלע CM היא גובה בטרפז ושווה לקטע DE שגם הוא גובה. לכן DE = 14.928 = CM.

BC = 26 - נתון

לכן:

sin(⦨CBM) = CM / BC = 14.928 / 26

⦨CBM = 35.04^°

ג. אורך הבסיס AB

אורך הבסיס AB הוא סכום הקטעים AE, BM, EM.

AE = 4 - נתון.

EM = CD = 8 - נתון כי CD = 8 ו - DE ו־ CM הם גבהים בטרפז. לכן המרובע CDEM הוא מלבן ולכן EM = CD.

לחישוב BM נתבונן במשולש ישר זווית BCM.

cos⦨CBM = BM / BC

BM = 26 ᐧ cos35.04^°= 21.28

AB = AE + EM + BM = 4 + 8 + 21.28 = 33.28

ד. שטח הטרפז ABCD .

שטח טרפז שווה למחצית סכום בסיסיו כפול הגובה. לכן שטח טרפז ABCD:

DE = 14.928 - חושב בסעיף א

CD = 8 - נתון

AB = 33.28

SABCD = (AB + CD) ᐧ DE /2 = (33.28 + 8) ᐧ 14.928 /2 = 308.11

שטח הטרפז ABCD הוא בקרוב 308.

דפים