תרגילים פתורים ממבחן חשבון מיצב תשסח ב - כיתה ח - חלק ב

שאלה 7 - ניתוח נתונים בגרף

במעדנייה מזמינים בכל יום מספר שונה של לחמניות.
בכל יום נמכרות חלק מהלחמניות, ואת הלחמניות שלא נמכרות תורמים למוסדות צדקה.
הגרף שלפניכם מתאר את מספר הלחמניות שהוזמנו ואת מספר הלחמניות שנמכרו בכל יום בשבוע עבודה אחד.

התבוננו בגרף וענו על הסעיפים שלפניכם:

א. מהו מספר הלחמניות שהוזמנו ביום שישי?
תשובה: ניתן לראות בגרף כי מספר הלחמניות שהוזמנו ביום ששי הור 55, לפי מיקום המעגל הריק (המסמל את מספר הלחמניות שהוזמנו) ששי על הציר האופקי (ציר x), ומיקום 55 על הציר האנכי (ציר y).

ב. ביום רביעי מסומן בגרף כך :   . מה יכולה להיות המשמעות של הסימון הזה?
תשובה: משמעות הסימול הוא הסימולים מעגל ריק וריבוע שחור באותה נקודה בגרף, כלומר באותו יום הוזמנו ונמכרו אותו מספר של לחמניות:  40


ג. באיזה יום תרמו את מספר הלחמניות הגדול ביותר?
תשובה: היום שבו תרמו את מספר הלחמניות הגדול ביותר הוא היום שבו ההפרש בין הכמות שהוזמנו לכמות שנמכרו הוא הגבוה ביותר. רואים זאת בגרף ביום ששי שבו המרחק בין הסימולים הוא הכי גדול.
30 = 25 - 55 , הכמות שנתרמה היא 30 לחמניות.


ד. באיזה יום לא נמכרו לחמניות כלל?
תשובה: לא נמכרו לחמניות כלל ביום שני. רואים זאת בגרף שבו הסימול ללחמניות שנמכרו (ריבוע שחור) מונח על ציר x - כלומר שווה .0

שאלה 8 - שטחים: משולש ישר זוית ומלבן

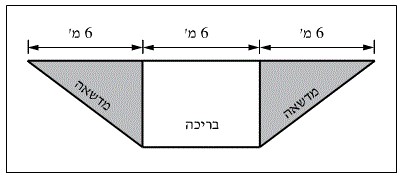
בסרטוט שלפניכם מוצגת תכנית של בריכה ושל מדשאות במרכז ספורט. הבריכה היא מלבנית ומשני צִדיה יש מדשאות בצורת משולשים ישרי-זווית. חלק מהמידות של המדשאות ושל הבריכה רשומות בסרטוט.
 

 מרכז הספורט

א. השטח של שתי המדשאות יחד:

 

1) שווה לשטח הבריכה.

2) קטן משטח הבריכה.

3) קטן משטח הבריכה.

 

ב. נמקו את תשובתכם.

 

פתרון

סעיף א - התשובה הנכונה היא 1. שטח שתי המדשאות יחד שווה לשטח הברכה.
סעיף ב - הסיבה לכך: הברכה היא מלבנית בעלת אורך 6 מ' ורוחב x, ולכן שטחה הוא 6x. כל מדשאה היא משולש ישר זוית בעל ניצב אחד באורך 6 מ', וניצב שני באורך x כמו רוחב הברכה. שטח משולש ישר זוית שווה למחצית מכפלת ניצביו, ולכן שטח כל מדשאה הוא: 6x/2.
שטח שתי המדשאות הוא: 6x/2 + 6x/2 = 6x וזה גם שטח הברכה.


שאלה 9 - פתרון בעיה עם משוואה אלגברית מעלה ראשונה בנעלם אחד

סכום הגילים של אב ובנו הוא 60. היחס בין גילו של הבן לגילו של האב הוא: 1:5. מה היה גילו של הבן לפני 4 שנים? הציגו את דרך הפתרון.

פתרון: נניח גיל האב הוא x. מכאן גיל הבן הוא  (x -ו60) , ויחס הגילאים הוא 5 כלומר: 

x / (60 - x)  = 5

נפתור את המשוואה:

x / (60 - x)  = 5

x  = 5ᐧ(60 - x)

x = 300 - 5x

6x = 300

x = 50

 גיל האב הוא 50, וגיל הבן הוא: 10 = 50 - 60.
גיל הבן לפני 4 שנים היה: 6 = 4 - 10



שאלה 10 - הצבת ערך מספרי במקום ביטוי בתבנית

נתון: x – y = 4
בהסתמך על הנתון, חשבו את ערכי הביטויים (התבניות) שלפניכם
והציגו את דרך החישוב.

פתרון
סעיף א - מציבים בתבניות את המספר 4 בכל מקום בו מופיע הביטוי x - y.
ונקבל:

סעיף ב -נפתור בדרך דומה:

שאלה  11 - הרכבת תבנית פסוק ופתרונה

 

נתון לוח מלבני שמידותיו מתוארות בסרטוט:

 

א. ממספר לוחות מלבניים הזהים במידותיהם ללוח הנתון, בנו שתי צורות שונות (ראה איור).

 

נתון: השטח של צורה א' גדול ב- 24 סמ"ר מהשטח של צורה ב'.
מצאו את ערכו של x בלוח הנתון והציגו את דרך הפתרון.

פתרון סעיף א

השטח של מלבן בודד הוא : 2x
צורה א מורכבת מ- 6 מלבנים לכן שטחה הוא: 12x =   6ᐧ2x

צורה ב מורכבת מ- 4 מלבנים לכן שטחה הוא: 8x =   4ᐧ2x

השטח של צורה א גדול ב- 24 סמ"ר מהשטח של צורה ב:
12x - 8x = 24
4x = 24
x = 6

קישורים:

תרגילים פתורים - מתוך מבחן מיצ"ב מתמטיקה כיתה ח' - תשע"א ב' - חלק א שאלות 1-6,
חלק ב שאלות 7-12, שאלות 13-15 , שאלה 18 , שאלה 21 , שאלה 24

תרגילים פתורים ממבחן מיצב תשס"ח ב - כיתה ח: חלק א,
מציאת קבוצת האמת של מערכת המשוואות
פתרון גרפי של שתי משוואות לינאריות עם שני נעלמים