שאלה 1
בעבודת חקר של תלמידי מגמת פיזיקה בבית ספר תיכון, החליטו התלמידים לבחון את מאפייני התנועה של גופים הנזרקים אנכית. לשם כך הם עלו על מגדל שגובהו H וזרקו באותו רגע שלושה כדורים זהים: B , A ו־ C.
כדור A נזרק כלפי מטה במהירות התחלתית שגודלה v0 , כדור B נזרק כלפי מעלה במהירות התחלתית שגודלה זהה לגודל המהירות ההתחלתית של כדור A , וכדור C שוחרר ממנוחה. שלושת הכדורים לא התנגשו במהלך תנועתם.
התלמידים קבעו את כיוון הציר האנכי החיובי כלפי מטה.
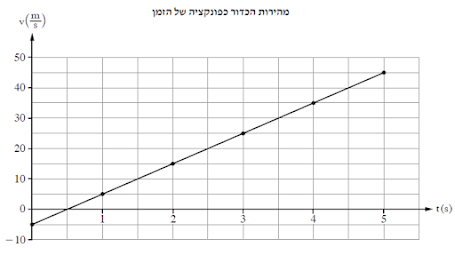
הם סרטטו גרף מהירות־זמן של אחד הכדורים מרגע זריקתו עד לסף פגיעתו בקרקע, כמתואר בתרשים שלפניך.
בסעיפים א-ד הנח כי כוח החיכוך בין הכדורים לאוויר ניתן להזנחה.
א. קבע אם הגרף מתאר את מהירותו של כדור A , כדור B או כדור C . נמק את קביעתך. ( 5 נקודות)
ב. חשב את גובה המגדל H . (חמש נקודות).
ג. חשב את המרחק האנכי בין מיקומו של כדור A לבין מיקומו של כדור B , בזמן t = 2s (שש נקודות)
התלמידים הוסיפו לאותה מערכת צירים את הגרפים המתאימים לשני הכדורים האחרים.
ד. הסבר מהי המשמעות הפיזיקלית של כל אחד מן הערכים (1) ו- (3) שלפניך, וקבע לאֵילו מן הערכים האלה יש גדלים מספריים זהים לכל שלושת הגרפים.
( 1) שיפוע הגרף
( 2) נקודת חיתוך הגרף עם ציר המהירות
( 3) השטח הכלוא בין הגרף לציר הזמן
( 6 נקודות)
ה. בסעיף זה הנח שבין כל כדור לאוויר פעל כוח חיכוך שגודלו קבוע וקטן ממשקל הכדור. להזכירך, כל
הכדורים זהים.
קבע אם גודל המהירות של כדור A ברגע פגיעתו בקרקע קטן מגודל המהירות של כדור B ברגע פגיעתו בקרקע, גדול ממנו או שווה לו. נמק את קביעתך באמצעות שיקולי אנרגיה או שיקולי קינמטיקה.
( 3 נקודות)
פתרון סעיף א
הגרף מתאר את מהירותו של כדור B שנזרק מעלה. מהירותו ההתחלתית היא שלילית, כלומר זריקה מעלה בכיוון השלילי . (הכיוון החיובי של ציר התנועה שקבעות התלמידים הוא מעלה). ניתן גם לראות שבשלב מסוים מהירות הכדור הופכת לחיובית, כלומר תנועתו מטה עקב כוח הכובד.
פתרון סעיף ב
נחשב את גובה המגדל על פי תנועתו של כדור B. (המידות בשניות, מטר, ומטר לשניה)
t = 5 - משך זמן התנועה של כדור B מרגע זריקתו מעלה ועד רגע פגיעתו בקרקע.
v0 = -5 - מהירותו ההתחלתית של כדור B היא 5- מטר לשניה (על פי הגרף).
V5 = 45 - מהירותו כעבור 5 שניות ברגע פגיעתו של כדור B בקרקע הוא 45 מטר לשניה.
נחשב את תאוצת הכדור:
תאוצת כדור B היא 10 מטר לשניה בריבוע.
נחשב את גובה המגדל שהוא המרחק x שעבר הכדור B (העתקה):
גובה המגדל הוא 100 מטר.
סעיף ג
נחשב את המרחק שעבר כל אחד מהכדורים (העתקה) ואח"כ נחשב את ההפרש.
חישוב המרחק שעבר כדור A
V0 = 5 - כדור A נזרק כלפי מטה (הכיוון החיובי) במהירות הזהה למהירות כדור B .
t = 2 - נתון
a = 10 - התאוצה חושבה בסעיף ב.
המרחק שעבר כדור A הוא 30 מטר.
חישוב המרחק שעבר כדור B
V0 = -5 - כדור B נזרק כלפי מעלה (הכיוון השלילי) .
t = 2 - נתון
a = 10 - התאוצה חושבה בסעיף ב.
המרחק שעבר כדור B הוא 10 מטר.
לפיכך המרחק האנכי בין כדור A לכדור B הוא 30-10 = 20 מטר
פתרון סעיף ד
(1) שיפוע הגרף הוא תאוצת הנפילה של הדורים שווה ערך ל- 10 מטר לשניה בריבוע.
(2) נקודת חיתוך הגרף עם ציר המהירות מציינת את המהירות בזמן t=0 כלומר המהירות ההתחלתית של הכדור וכיוונה בהתאם למיקום הנקודה (על הצד החיובי של ציר המהירות או השלילי).
(3) השטח הכלוא בין הגרף לציר הזמן מציין את המרחק (העתקה) שעבר הכדור בכיוון התנועה החיובי (כיוון מטה).