שאלה מספר 3
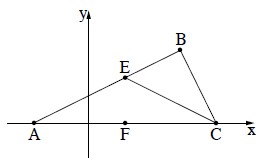
במשולש ABC הקודקודים A ו־ C מונחים על ציר ה־ x , כמתואר בסרטוט שלפניכם.
הנקודה E נמצאת על הצלע AB.
נתון: משוואת הישר AB היא y = (½)x +3
שיעור ה־ y של קודקוד B הוא 8 .
א. (1) מצאו את שיעורי הקודקוד A.
(2) מצאו את שיעור ה־ x של קודקוד B.
נתון: שיעורי הקודקוד C הם ( 0 , 14 ) .
ב. הוכיחו כי הצלע AB מאונכת לצלע . BC
נתון: שיפוע הישר EC הוא ½-
ג. (1) מצאו את משוואת הישר EC.
(2) מצאו את שיעורי הנקודה E.
ד. חשבו את שטח המשולש EBC.
הנקודה F נמצאת על ציר ה־ x כך שהקטע EF מקביל לציר ה־y.
ה. חשבו את שטח המרובע FEBC.
פתרון שאלה מספר 3
א. (1) שיעור הנקודה A
משוואת הישר AB היא : y = (½)x +3 .
נקודה A היא נקודת חיתוך עם ציר x. לכן מציב y = 0 במשוואת הישר AB לקבלת הנקודה :
y = (½)x +3
0 = (½)x +3 <= , y = 0
x = -6
שיעור הנקודה A הוא: (0 , 6-).
(2) . שיעור ה- x של הנקודה B
שיעור ה- y של הנקודה B נתון y = 8 . נציב במשוואת הישר AB , את הערך y = 8 ונקבל:
y = (½)x +3
8 = (½)x +3 <= , y = 8
x = 10
שיעור ה- x של הנקודה B הוא x = 10 , שיעור נקודה B הוא (8 , 10).
ב. הוכחת מאונכות הצלעות AB, BC
במערכת צירים שיפוע הישר המאונך לישר בעל שיפוע a הוא : a⅟- .
השיפוע a1 של הישר AB העובר דרך הנקודות A (-6 ,0) והנקודה B (10 , 8) , הוא:
a1 = - (8-0) / [10 - (-6)] = 8/16 = 1/2
רואים זאת גם מידית ממשוואת הישר AB שהיא : y = (½)x +3 .
באופן דומה אפשר למצוא את שיפוע a2 של הישר BC העובר דרך הנקודות B ו- C.
B (10, 8) , C (14 , 0)
a2 = (0-8) / (14-10) = -8/4 = -2
ניתן לראות כי a1 = -1/a2 לכן הישרים AB ו- BC מאונכים.
ג. (1) משוואת הישר EC
שיפוע הישר EC הוא : a = -1/2
הישר EC עובר דרך הנקודה C (14, 0) .
משוואת ישר ששיפועו a ועובר דרך נקודה (x1 , y1) הוא:
y - y1 = a(x - x1)
נציב ונקבל:
y - 0 = (-1/2)(x - 14)
y = (-1/2)x + 7
(2) שיעור הנקודה E
הנקודה E היא חיתוך הישרים:
AB : y = (1/2)x + 3
EC : y = (-1/2)x + 7
נפתור את המשוואות למציאת שיעור הנקודה E.
ניתן לראות מיידית מסיכום שתי המשוואות ש: 2y = 10 או y = 5.
המשך הפתרון יוביל ל x= 4
שיעור הנקודה E הוא: (5 , 4).
ד. שטח המשולש EBC.
המשולש EBC הוא משולש ישר זווית (BE , BC ניצבים, זווית B ישרה), לכן שיטחו: 2 / (BE * BC) .
נחשב את אורכי הניצבים BE , BC על מרחקים בין הנקודות B, C , E:
(8 , 10) B - חושב בסעיף א.(2)
(0 , 14) C - נתון.
(5 ֶ 4) E - חושב ב- א.(2)
שטח משולש BEC הוא 30 יחידות.
ה. שטח המרובע FEBC
שטח המרובע FEBC הוא סכום שטחי המשולשים BEC ו- EFC.
שטח המשולש BEC חושב בסעיף ד והוא 30 יחידות.
שטח המשולש EFC
FE מקביל לציר y ו- FC על ציר x, לכן משולש EFC הוא משולש ישר זווית (זווית EFC ישרה).
שיעור הנקודה E חושב ב- ג.(2) והוא (5 , 4), לכן EF = 5.
שיעור ה- x של נקודות E ו- F זהים מאחר והקטה EF מקביל לציר y, בנוסף נקודה F נמצאת על ציר x,
לכן שיעור הנקודה F הוא (0 , 4).
שיעור הנקודה C נתון (0, 14).
CF = 14 - 4 = 10
שטח משולש EFC
משולש EFC הוא ישר זווית מאחר והניצב CF מונח על ציר x, והניצב EF מקביל לציר y (נתון).
שטח משולש EFC = (CF * EF) / 2 = (10 * 5) /2 = 25
שטח מרובע FEBC
שטח מרובע FEBC = שטח משולש BEC + שטח משולש EFC =
30 + 25 = 55
שטח מרובע FEBC הוא 55.
אין תגובות:
הוסף רשומת תגובה