מעגל, משיק ומשולש - בגרות 4 יחידות מתמטיקה חורף 2022

מבחן בגרות מתמטיקה 4 יחידות חורף 2022 - שאלון ראשון

שאלה מספר 2

הנקודה M היא מרכז המעגל שמשוואתו

(x - 4)² + (y-3)² = 10

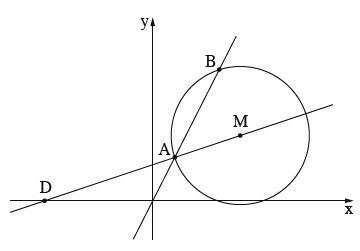
הישר y=2x חותך את המעגל בנקודות A ו־ B , כמתואר בסרטוט שלפניך.

א. מצא את שיעורי הנקודות A ו־  B.

הישר AM חותך את ציר ה־ x בנקודה D (ראה סרטוט).

ב. מצא את שיעורי הנקודה D.

ג. הוכח כי BM מאונך ל־  DM.

ד. האם הישר DB משיק למעגל? נמק.

ה. חשב את שטח המשולש ABD.

 פתרון שאלה 2

א. שיעורי הנקודות A ו - B.

הנקודות A, B הן נקודות חיתוך של מעגל M והישר y = 2x. לכן הנקודות A, B הן פתרון המשוואות המעגל M והישר y = 2x.

נפתור:

(x - 4)² + (y - 3)² = 10

y = 2x

נציב y = 2x במשוואת המעגל ונפתור:

(x - 4)² + (2x - 3)² = 10

x² - 8x + 16 + 4x² - 12x + 9 =10

5x² - 20x + 25 = 10

5ᐧx² - 20x + 15 = 0

x² - 4x + 3 = 0

(x - 1)(x - 3) = 0

קיבלנו 2 שורשים : x1 = 3 , x2 = 1

מאחר ו- y = 2x , נציב ונקבל: y1 = 6 , y2 = 2 .

לכן שיעור הנקודה A הוא: (2, 1)

שיעור הנקודה B הוא: (6, 3)

 

ב. שיעורי הנקודה D.

הנקודה D היא נקודת חיתוך הישר העובר דרך הנקודות M, A עם ציר x.

שיעור הנקודה A חושב בסעיף א : (2 , 1)

ע"פ משוואת המעגל  M :

(x - 4)² + (y - 3)² = 10

שיעור מרכז המעקגל הנקודה M הוא: (3 , 4)

לכן משוואת הישר העובר דרך הנקודות A, M : 

 

משוואת הישר העובר דרך הנקודות M, A היא  3y = x+5.

נקודת חיתוך D של ישר זה עם ציר x היא כאשר  y=0 כלומר:

x + 5 = 0

x = -5

שיעור נקודה D הוא (0 , 5-).

 

 

ג. הוכח כי BM מאונך ל־  DM.

 נחשב שיפוע כל אחד מהקטעים BM, DM, ונבדוק אם הם מקיימים את יחס המאונכות, כלומר מכפלת השיפועים שווה 1-.

נשתמש בנוסחה למציאת שיפוע m של ישר העובר דרך שתי נקודות

השיפוע m נתון בנוסחה: 

שיפוע BM 

שיעור הנקודה B הוא: (6, 3).  חושב בסעיף א.

שיעור M מרכז המעגל שמשוואתו

  (x - 4)² + (y - 3)² = 10  

נובע מידית מהמשוואה.

שיעור הנקודה M הוא  (3 , 4).

 שיפוע BM  הוא :

  (3-4)/(6-3) = 3-

שיפוע DM 

שיעור הנקודה M הוא  (3 , 4).  חושב בסעיף ג.

שיעור נקודה D הוא (0 , 5-). חושב בסעיף ב.

שיפוע DM הוא:   (4+5)/(3-0) = 1/3

שיפועי הקטעים DM, BM מקיימים את יחס המאונכות הואיל ומכפלתם היא 1- = (3-)*1/3

לכן הקטעים DM, BM מאונכים.

ד. האם הישר DB משיק למעגל? נמק.

נשתמש במשפט מאונכות הרדיוס למשיק למעגל בנקודת ההשקה ונבדוק האם הישר DB מאונך לרדיוס MB בנקודת מפגש על המעגל. בדיקת המאונכות תעשה על ידי בדיקת יחס השיפועים. כלומר אם מכפלת שיפוע הישר DB ברדיוס MB שווה 1- אזי DB מאונך לרדיוס MB ולכן DB משיק למעגל.

שיעורי הנקודות M, B , D.

שיעור הנקודה M הוא  (3 , 4). חושב בסעיף ג.

שיעור הנקודה B הוא: (6, 3).  חושב בסעיף א.

שיעור נקודה D הוא (0 , 5-). חושב בסעיף ב.4

חישוב שיפועי  BD, DM:

 שיפוע BM : 

(4-3) / (3-6) = 3-

 שיפוע DB:

(3+5)/(6-0) = 3/4

מכפלת שיפועי BM, DB:

(3-) * (3/4) = 4 / 9- = 2.25- שונה מ- 1-, לכן DB, BM אינם מאונכים והישר DB אינו משיק למעגל M.

ה. שטח המשולש ABD

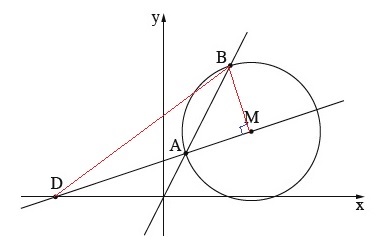
 למציאת שטח משולש ABD, נבנה בניות עזר את הקטעים BM, AD.

נחשב את שטח המשולש ABD כהפרש שטחי המשולשים MBD, ABM. נוכל להעזר בתכונה שהם משולשים ישרי זוית כפי שהוכחנו בסעיף ג שקטע BM מאונך ל DM.

שטח משולש ABM:

משולש ABM הוא ישר זוית (זוית M) כפי שהוכח בסעיף ג.

ניצבי המשולש ABM הם רדיוסים של המעגל M. והם מאונכים בנקודה M.

אורך הניצבים AM, BM הוא . על פי נוסחת משוואת המעגל: 

(x - 4)² + (y - 3)² = 10

לכן שטח המשולש ABM הוא AMᐧBM/2 = 10 / 2 = 5

 שטח משולש BDM

נמצא את אורכו של MD. שיעור נקודה D הוא (0 , 5- ) , ושיעור נקודה M הוא: (3 , 4) . 

על פי נוסחת מרחק בין שתי נקודות במערכת צירים, המרחק d בין הנקודות M, D:

 אורך DM הוא:

 אורך BM הוא רדיוס המעגל שווה .

משולש BDM הוא ישר זווית מאחר וזווית M ישרה (הוכח סעיף ג).

לכן שטח S משולש BDM:

 שטח משולש ABD הוא הפרש שטחי המשולשים MBD, ABM. לכן שטחו: 15-5 = 10

 שטח משולש ABD הוא 10.