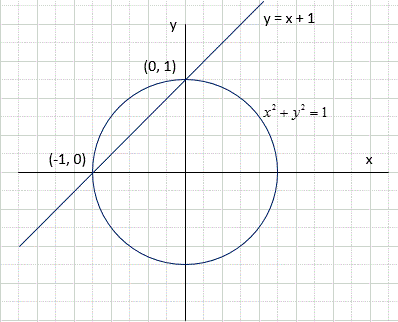משיק למעגל - מונחים ומשפטים

הגדרה - משיק למעגל, נקודת השקה

 

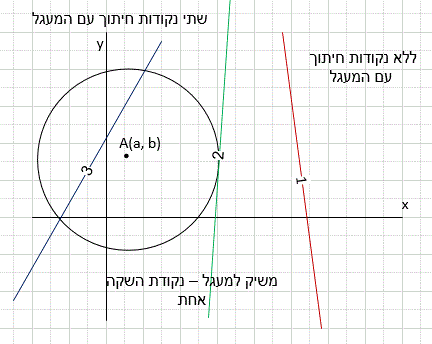
ישר שיש לו רק נקודה אחת משותפת עם המעגל נקרא משיק למעגל. הנקודה המשותפת נקראת נקודת ההשקה או נקודת המגע.
בסקיצה להלן הישר l משיק למעגל O בקודת ההשקה A.

ישר l משיק למעגל O בנקודת ההשקה A

משפטים:

משיק למעגל מאונך לרדיוס העובר בנקודת ההשקה
נניח מעגל O ומשיק a למעגל בנקודת השקה A, אזי רדיוס המעגל OA מאונך למשיק a .
המשפט ההפוך תקף גם: ישר המאונך לרדיוס בקצהו משיק למעגל

 

משיק למעגל מאונך לרדיוס העובר בנקודת ההשקה

משפטים נוספים:

 
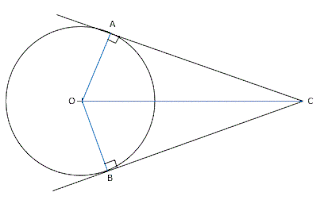
נניח שני משיקים ( AC, BC) היוצאים למעגל מנקודה C מחוץ למעגל O. מתקימות שתי תכונות:
1. המשיקים שווים: AC = BC
2. הקטע המחבר את מרכז המעגל עם הנקודה ממנה יוצאים המשיקים חוצה את הזוית בין שני המשיקים. כלומר: הקטע OC חוצה זוית C :
זווית C1 = זווית C2

משפט - זווית בין משיק למיתר

 

 

הזווית בין משיק למיתר הנפגשים בנקודת ההשקה שווה לזווית ההיקפית הנשענת על המיתר מצידו השני

 נתון מעגל שמרכזו בנקודה O
AB מיתר במעגל, ו- l משיק למעגל בנקודה A

מכאן שזווית היקפית כלשהי  ᵧ (זווית ACB) הנשענת על מיתר AB שווה לזווית α  (זווית BAl) בין משיק l למיתר AB.
  ᵧ = α

הוכח: אם מנקודה שמחוץ למעגל יוצאים שני משיקים למעגל, אז הקטע המחבר את מרכז המעגל עם הנקודה שממנה יוצאים שני המשיקים חוצה את הזווית שבין המשיקים.

נתון 

מעגל שמרכזו הנקודה  O ,

AC משיק למעגל O בנקודה A

BC משיק למעגל O בנקודה B

OC - הקטע המחבר את מרכז המעגל O עם הנקודה C שממנה יוצאים שני המשיקים.

שני משיקים מנקודה שמחוץ למעגל והקטע המחבר את מרכז המעגל עם הנקודה

צריך להוכיח

זוית OCA (זוית C1) = זוית OCB (זוית  C2)

הוכחה

שיטת ההוכחה
בונים בניית עזר הרדיוסים OA, OB, והקטע OC וחופפים משולשים AOC, BOC ע"פ משפט חפיפה רביעי. מהחפיפה נובע כי הזויות C1, C2 שוות.

בניית עזר

בונים בניית עזר הרדיוסים OA, OB, והקטע OC

שני משיקים היוצאים מנקודה C מחוץ למעגל O והרדיוסים המאונכים להם

 

חפיפת משולשים AOC, BOC

1: AB = BO - רדיוסים במעגל O - ראה בניית עזר

2: CO = CO - צלע משותפת

3: זוית OAC = זוית OBC = 90 מעלות - זויות בין הרדיוסים OA, OB למשיקים CA, CB בהתאמה שוות 90 מעלות.

מכאן:
משולשים AOC, BOC חופפים - נובע מ- 1,2,3 ע"פ משפט חפיפה רביעי

מהחפיפה נובע: זוית C1 = זוית C2

מ.ש.ל

שני משיקים למעגל היוצאים מאותה נקודה שווים זה לזה

נתון 

מעגל שמרכזו הנקודה O
AC משיק למעגל O בנקודה A
BC משיק למעגל O בנקודה B

שני משיקים למעגל היוצאים מאותה נקודה

 

צריך להוכיח

AC = BC

הוכחה

שיטת ההוכחה
בונים בניית עזר הרדיוסים OA, OB, והקטע OC וחופפים משולשים AOC, BOC ע"פ משפט חפיפה רביעי. מהחפיפה נובע כי AC = BC.

בניית עזר
בונים בניית עזר הרדיוסים OA, OB, והקטע OC

בניית עזר הרדיוסים OA, OB, והקטע OC

 

חפיפת משולשים AOC, BOC
1: AB = BO - רדיוסים במעגל O - ראה בניית עזר
2: CO = CO - צלע משותפת
3: זוית OAC = זוית OBC = 90 מעלות - זויות בין הרדיוסים OA, OB למשיקים CA, CB בהתאמה שוות 90 מעלות.

מכאן:
משולשים AOC, BOC חופפים - נובע מ- 1,2,3 ע"פ משפט חפיפה רביעי

מהחפיפה נובע: AC = BC

מ.ש.ל

הוכח: ישר המאונך לרדיוס בקצהו משיק למעגל.

נתון

 
מעגל שמרכזו נקודה O

 

ישר מאונך לרדיוס בקצהו

 

 

1. AO רדיוס המעגל,
2.  A נקודת החיבור של הרדיוס עם הישר l.
3. l מאונך ל-AO.

צריך להוכיח

 
l משיק למעגל O

 הוכחה

נוכיח בדרך השלילה. נניח כי הישר l אינו משיק למעגל, וחותך את המעגל בנקודה נוספת B.

ב.ע. BO רדיוס לנקודת החיתוך הנוספת

 

4.  ב.ע. BO רדיוס לנקודת החיתוך הנוספת.
${\displaystyle \ BO=AO}$5. AO = BO  - כל הרדיוסים במעגל O שווים
6. זוית OAB = זוית OBA - זויות בסיס במשולש שווה שוקיים OAB שוות - נובע מסעיף 5
7. זוית OAB = 90 מעלות - נתון (סעיף 3)
8. זוית OBA = 90 מעלות - נובע מ- 6, 7
9. קיבלנו סתירה (סכום הזווית במשולש ABO גדול מ-180, לפי 8).

 מכאן של- l נקודה משותפת אחת עם מעגל O ולכן הוא משיק

מ.ש.ל

ישר ומעגל במערכת צירים

נניח מעגל במערכת צירים שמרכזו בנקודה A(a ,b) רדיוסו r. במערכת הצירים ישנו גם ישר y = mx +n. 

מעגל במערכת צירים שמרכזו בנקודה A(a ,b) רדיוסו r. במערכת הצירים ישנו גם ישר y = mx +n .

1: משוואת המעגל שמרכזו בנקודה A(a ,b) ורדיוסו r :

(x - a)² + (y - b)² = r²

2: משוואת הישר:  y = mx + n

ישנם שלשה מצבים אפשריים בין הישר למעגל:
1. הישר אינו חותך את המעגל באף נקודה ולמשוואות 1, 2 לעיל אין פתרון.
2. הישר משיק למעגל (נקודת חיתוך אחת) ולמשוואות 1, 2 לעיל פתרון אחד.
3. הישר חותך את המעגל בשתי נקודות ולמשוואות 1, 2 שתי פתרונות.

 דוגמא 1:
 נתון המעגל  x² + y²  = 1 וישר  y = x + 1

מצא כמה נקודות חיתוך לישר ולמעגל.

פתרון 1

פותרים את המשוואות ובודקים כמה פתרונות מקבלים:

 x² + y²  = 1

y = x + 1

 x² + (x + 1)²  = 1

 x² +  x² + 2x + 1 = 1

 2x² + 2x = 0

 x² + x = 0

x(x + 1) = 0

x₁ = 0

x₂ = -1

y = x + 1

y₁ = 1

y₂ = 0

קיבלנו שני פתרונות ולכן הישר והמעגל נחתכים בשתי נקודות שהן: (1 ,0) , (0 ,1-).

להלן גרף הישר והמעגל:

סקיצה - ישר ומעגל נחתכים בשתי נקודות חיתוך במערכת צירים

משוואת המעגל

מעגל שמרכזו בנקודה a,b ורדיוסו r

 

נתון מעגל שמרכזו בנקודה P(a, b) , רדיוס המעגל הוא r. ניתן למצוא את משוואת המעגל ע"י מציאת המקום הגאומטרי של נקודות המישור הנמצאות על המעגל.

נתבונן בנקודה כלשהי C(x, y) .
המבחן אם נקודה C על המעגל הוא שמרחקה ממרכז המעגל נקודה P(a,b) הוא r. כלומר:


או

 (x- a)² + (y - b)² = r²

ומצאנו את משוואת המעגל.

נוכל לסכם: משוואת מעגל שמרכזו בנקודות (a, b) ורדיוסו r , היא:

 (x- a)² + (y - b)² = r²

דוגמא 1:

מהי משוואת המעגל שרדיוסו 5 יחידות ושיעור מרכזו בנקודה (2, 6)

פתרון 1 :
משוואת מעגל שמרכזו בנקודות (a, b) ורדיוסו r , היא:  

 (x- a)² + (y - b)² = r²

נציב:
a = 6
b = 2
r = 5

ונקבל:

(x- 6)² + (y - 2)² = 5²

(x- 6)² + (y - 2)² = 25

משוואת המעגל:

 (x- 6)² + (y - 2)² = 25

דוגמא 2
המשוואה  x² - 5x + y² = 0 מייצגת מעגל. מצא את שיעור מרכז המעגל ואורך רדיוסו.

פתרון 2

נפתח את משוואת המעגל  x² - 5x + y² = 0 לצורה

 (x- a)² + (y - b)² = r²

 ומצאנו את רדיוס המעגל r ושיעור מרכז המעגל (a, b).

x² - 5x + y² = 0

x² - 5x + 25 - 25 + y² = 0

(x - 5)² + (y - 0)² = 25

(x - 5)² + (y - 0)² = 5²

 קיבלנו כי רדיוס המעגל שווה 5 יחידות ושיעור מרכזו (0, 5)