מחומש מורכב ממשולש מחובר לריבוע - ממבחן מיצב כיתה ח תשע"א

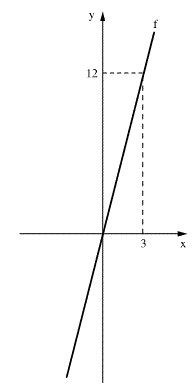
שאלה 21
לפניכם שרטוט של מחומש ABCDE המורכב מריבוע ABDE וממשולש ישר-זווית BCD.

מבחן מיצב כיתה ח - מחומש מורכב מריבוע ומשולש ישר זווית

א. מה שטח הריבוע ABDE? הציגו את דרך הפתרון:

 
פתרון סעיף א
נמצא תחילה את אורך צלע BD של הריבוע ABDE, ע"פ משפט פיתגורס.
משולש  BCD ישר זוית (זוית C ישרה) לכן סכום ריבועי הניצבים BC, ו- CD שווה לריבוע היתר BD:

BD² = BC² + CD²

או בהצבה ופתרון:

BD² = 7² + 5²

BD² = 49 + 25 = 74

BD = √74

שטח ריבוע שווה לריבוע צלע מצלעותיו השוות, בעצמה:

שטח הריבוע :     S = BD² = 74


ב. מה שטח המחומש ABCDE? הציגו את דרך הפתרון:

פתרון סעיף ב
שטח המחומש ABCDE מורכב משטח הריבוע ABDE ושטח המשולש ישר הזוית BCD. נמצא את שטח הריבוע ושטח המשולש, נחבר אותם, ונקבל את שטח המחומש.
שטח ריבוע ABDE -מצאנו בסעיף א: S = BD² = 74
שטח המשולש BCD - שטח משולש שווה למחצית מכפלת צלע בגובה לאותה הצלע. כאשר המשולש ישר זוית, הניצבים מהווים צלעות וגבהים אחד לשני, לכן שטח משולש ישר זוית שווה למחצית מכפלת ניצביו.

שטח משולש BCD:

S_BCD = ½ ᐧ BC ᐧ CD = ½ ᐧ 7 ᐧ 5 = 17.5

שטח המחומש ABCDE הוא סכום שטח הריבוע ושטח המשולש: 91.5 = 74 + 17.5


ג. מה היקף המחומש ABCDE?

פתרון סעיף ג
היקף המחומש P שווה לסכום אורכי צלעותיו:

P = AB + BC + CD + DE + AE

P = √74 + 7 + 5 + √74 + √74

P = 3√74 + 12

התשובה הנכונה היא מספר 3.

קישורים:

• תרגילים פתורים ממבחן מיצב תשסח ב - כיתה ח - חלק ב

מבחן מיצב כיתה ח תשס"א פתרונות שאלות 13-15

שאלה מספר 13

פִּתרו את המשוואה שלפניכם, הציגו את דרך הפתרון:

(2x + 8) / 6 - x = (x + 10) / 3

פתרון שאלה 13

(2x + 8) / 6 - x = (x + 10) / 3

כופלים כל האגפים ב- 6:

2x + 8 - 6x = 2(x + 10)
2x + 8 - 6x = 2x + 20
6x = -12

x = -2

שאלה מספר 14

פתרון שאלה 14

הוכחה

1. - נובע מחפיפת משולשים ABC, AFD
2 . - נתון
3. - נובע מ- 1 ו-2 , בהצבה
נתבונן בזויות המשולש AFD, סכומן 180 מעלות, לכן:

4. - סכום זויות במשולש הוא 180 מעלות
5. אך זויות FAD, AFD שוות 25 , 80 מעלות בהתאמה - נתון והוכח ב- 3
6. מכאן זוית ADF שווה 180-80-25 = 75 מעלות - נובע מ-4 , 5

שאלה מספר  15 - שיפוע גרף ישר ומציאת משוואת הישר

לפניכם גרף המתאר את הפונקציה הקווית f.

א. מה שיפוע הישר?

תשובה _______________ 

 

ב. כתבו פונקציה g שהגרף המתאר אותה הוא ישר המקביל לגרף הפונקציה f , 

ועובר דרך הנקודה (12 , 0).

פתרון שאלה 15

סעיף א - משוואת הפונקציה הקווית f היא y = ax +b כאשר a הוא שיפוע הגרף ו- b היא נקודת חיתוך עם ציר y.
במקרה לפנינו הגרף עובר דרך ראשית הצירים נקודה (0,0) ולכן b =0 .
הגרף עובר גם דרך הנקודה (3,12) ולכן נציב המשוואה y = ax ונקבל 12 = 3a , או a = 4 , כלומר שיפוע הגרף הוא 4.
סעיף ב - הפונקציה g היא גרף ישר המקבילה ל- f , לכן יש לה אותו שיפוע a = 4 . נקודת חיתוך של g עם ציר y היא (0,12) לכן b = 12.
משוואת פונקציית הישר g היא מהצורה: y = ax +b , כלומר: y = 4x +12
שרטוט הפונקציות f,g: ( הפונק' g בצבע כחול)

שרטוט הפונקציות f,g: ( הפונק' g בצבע כחול)

שאלה 16

גנן תכנן להרכיב צינור מים מארבעה חלקים, ולהניח אותו בגינה שאורכה 5 מטרים.

האורך הכולל של הצינור צריך להיות קצר מאורך הגינה.

הגנן הניח חלק אחד שאורכו 2.3 מטרים, וחיבר אליו עוד שלושה חלקים אחרים השווים באורכם זה לזה, כפי שמתואר בסרטוט. x מייצג את האורך במטרים של כל אחד משלושת החלקים השווים באורכם.

 
א. כִּתבו שני אורכים אפשריים שונים לחלק של הצינור שאורכו מיוצג על ידי x.

פתרון סעיף 16.א

אורך כל החלקים יחד צריך להיות קטן מ-5 מ', כלומר הסכום של החלק האחד באורך 2.3 מ' ועוד 3 חלקים שווים באורך x קטן מ- 5 מ'.
ניתן לתאר את השאלה באי שיוויון: 

2.3 + 3x < 5

נפתור את אי השיוויון:

2.3 + 3x < 5
3x < 5 - 2.3
3x < 2.7

x < 0.9

x חייב להיות קטן מ- 0.9 מ'.
אורכים אפשריים ל- x : 
0.8מ', 0.6 מ'.


ב. סַמנו את האי-שוויון המתאים לנתוני השאלה.

 

 פתרון סעיף 16.ב

תשובה: כפי שענינו בסעיף 1 לעיל התשובה הנכונה היא 2:

2.3 + 3x < 5

תרגילים פתורים ממבחן חשבון מיצב תשסח ב - כיתה ח - חלק ב

שאלה 7 - ניתוח נתונים בגרף

במעדנייה מזמינים בכל יום מספר שונה של לחמניות.
בכל יום נמכרות חלק מהלחמניות, ואת הלחמניות שלא נמכרות תורמים למוסדות צדקה.
הגרף שלפניכם מתאר את מספר הלחמניות שהוזמנו ואת מספר הלחמניות שנמכרו בכל יום בשבוע עבודה אחד.

התבוננו בגרף וענו על הסעיפים שלפניכם:

א. מהו מספר הלחמניות שהוזמנו ביום שישי?
תשובה: ניתן לראות בגרף כי מספר הלחמניות שהוזמנו ביום ששי הור 55, לפי מיקום המעגל הריק (המסמל את מספר הלחמניות שהוזמנו) ששי על הציר האופקי (ציר x), ומיקום 55 על הציר האנכי (ציר y).

ב. ביום רביעי מסומן בגרף כך :   . מה יכולה להיות המשמעות של הסימון הזה?
תשובה: משמעות הסימול הוא הסימולים מעגל ריק וריבוע שחור באותה נקודה בגרף, כלומר באותו יום הוזמנו ונמכרו אותו מספר של לחמניות:  40


ג. באיזה יום תרמו את מספר הלחמניות הגדול ביותר?
תשובה: היום שבו תרמו את מספר הלחמניות הגדול ביותר הוא היום שבו ההפרש בין הכמות שהוזמנו לכמות שנמכרו הוא הגבוה ביותר. רואים זאת בגרף ביום ששי שבו המרחק בין הסימולים הוא הכי גדול.
30 = 25 - 55 , הכמות שנתרמה היא 30 לחמניות.


ד. באיזה יום לא נמכרו לחמניות כלל?
תשובה: לא נמכרו לחמניות כלל ביום שני. רואים זאת בגרף שבו הסימול ללחמניות שנמכרו (ריבוע שחור) מונח על ציר x - כלומר שווה .0

שאלה 8 - שטחים: משולש ישר זוית ומלבן

בסרטוט שלפניכם מוצגת תכנית של בריכה ושל מדשאות במרכז ספורט. הבריכה היא מלבנית ומשני צִדיה יש מדשאות בצורת משולשים ישרי-זווית. חלק מהמידות של המדשאות ושל הבריכה רשומות בסרטוט.
 

 מרכז הספורט

א. השטח של שתי המדשאות יחד:

 

1) שווה לשטח הבריכה.

2) קטן משטח הבריכה.

3) קטן משטח הבריכה.

 

ב. נמקו את תשובתכם.

 

פתרון

סעיף א - התשובה הנכונה היא 1. שטח שתי המדשאות יחד שווה לשטח הברכה.
סעיף ב - הסיבה לכך: הברכה היא מלבנית בעלת אורך 6 מ' ורוחב x, ולכן שטחה הוא 6x. כל מדשאה היא משולש ישר זוית בעל ניצב אחד באורך 6 מ', וניצב שני באורך x כמו רוחב הברכה. שטח משולש ישר זוית שווה למחצית מכפלת ניצביו, ולכן שטח כל מדשאה הוא: 6x/2.
שטח שתי המדשאות הוא: 6x/2 + 6x/2 = 6x וזה גם שטח הברכה.


שאלה 9 - פתרון בעיה עם משוואה אלגברית מעלה ראשונה בנעלם אחד

סכום הגילים של אב ובנו הוא 60. היחס בין גילו של הבן לגילו של האב הוא: 1:5. מה היה גילו של הבן לפני 4 שנים? הציגו את דרך הפתרון.

פתרון: נניח גיל האב הוא x. מכאן גיל הבן הוא  (x -ו60) , ויחס הגילאים הוא 5 כלומר: 

x / (60 - x)  = 5

נפתור את המשוואה:

x / (60 - x)  = 5

x  = 5ᐧ(60 - x)

x = 300 - 5x

6x = 300

x = 50

 גיל האב הוא 50, וגיל הבן הוא: 10 = 50 - 60.
גיל הבן לפני 4 שנים היה: 6 = 4 - 10



שאלה 10 - הצבת ערך מספרי במקום ביטוי בתבנית

נתון: x – y = 4
בהסתמך על הנתון, חשבו את ערכי הביטויים (התבניות) שלפניכם
והציגו את דרך החישוב.

פתרון
סעיף א - מציבים בתבניות את המספר 4 בכל מקום בו מופיע הביטוי x - y.
ונקבל:

סעיף ב -נפתור בדרך דומה:

שאלה  11 - הרכבת תבנית פסוק ופתרונה

 

נתון לוח מלבני שמידותיו מתוארות בסרטוט:

 

א. ממספר לוחות מלבניים הזהים במידותיהם ללוח הנתון, בנו שתי צורות שונות (ראה איור).

 

נתון: השטח של צורה א' גדול ב- 24 סמ"ר מהשטח של צורה ב'.
מצאו את ערכו של x בלוח הנתון והציגו את דרך הפתרון.

פתרון סעיף א

השטח של מלבן בודד הוא : 2x
צורה א מורכבת מ- 6 מלבנים לכן שטחה הוא: 12x =   6ᐧ2x

צורה ב מורכבת מ- 4 מלבנים לכן שטחה הוא: 8x =   4ᐧ2x

השטח של צורה א גדול ב- 24 סמ"ר מהשטח של צורה ב:
12x - 8x = 24
4x = 24
x = 6

קישורים:

תרגילים פתורים - מתוך מבחן מיצ"ב מתמטיקה כיתה ח' - תשע"א ב' - חלק א שאלות 1-6,
חלק ב שאלות 7-12, שאלות 13-15 , שאלה 18 , שאלה 21 , שאלה 24

תרגילים פתורים ממבחן מיצב תשס"ח ב - כיתה ח: חלק א,
מציאת קבוצת האמת של מערכת המשוואות
פתרון גרפי של שתי משוואות לינאריות עם שני נעלמים

דוגמאות פתורות מבחן מפמ"ר מתמטיקה כיתה ט - רמה רגילה תשע"ב - שאלות 1-6

שאלה מספר 1 -  פתרו את המשוואה הבאה בשתי דרכים: 

2(x - 4)² = 18

פתרון

דרך ראשונה:

 

דרך שניה

2(x - 4)² = 18

(x - 4)² = 9

x - 4 = ± 3

x1 = 3 + 4 = 7

x2 = -3 + 4 = 1

שאלה מספר 2 - הסבירו מדוע למשוואה

(x + 5)² + 5 = 0

אין פתרון

תשובה

נפתח את המשוואה

(x + 5)² + 5 = 0

(x + 5)²  = - 5

קיבלנו באגף השמאלי ביטוי ²(x + 5) שהוא ריבוע מספר ולכן חייב להיות חיובי.

מאידך באגף הימני המספר 5- שלילי.
מכאן למשוואה סתירה לוגית ולכן אין לה פתרון.


 שאלה מספר 3

פתור את המשוואה במספר דרכים
דרך 1 - פתיחת סוגריים וכינוס איברים:

דרך 2 - משתמשים בנוסחת כפל מקוצר:

דרך 3 - הוצאת שורשים מידית

נבדוק עבור כל אפשרות: שורש חיובי ושורש שלילי

 שורש חיובי:

קיבלנו סתירה לוגית, אין פתרון עבור x באפשרות זאת

שורש שלילי

פתרון 0 = x

שאלה מספר 4
פתור את המשוואות, רשום תחום הצבה, ובדוק הפתרון באמצעות הצבה

 

פתרון
תחום ההצבה הוא התחום בו לביטויים המרכיבים את המשוואה יש ערכים מוגדרים. כאשר למכנה יש ערך 0 הביטוי לא מוגדר ואינו בתחום ההצבה. המכנים במשוואות האלו הם: 3 - x , ו- (6 - 2x).
 מכנים אלו שונים מאפס כאשר x שונה מ- 3 לכן תחום ההצבה בוא כל המספרים פרט ל- 3 = x, מסמנים זאת כך:

פתרון המשוואה:

בדיקה: נציב במשוואה   את הערך 5 = x

קיבלנו שוויון אמת 6 =6 , ולכן הפתרון 5 = x נכון.



שאלה מספר 5
 פתור את המשוואה:

פתרון: פותחים סוגריים מכנסים איברים ומקבלים משוואה ריבועית. מהסוג:

מציבים בנוסחת השורשים:

ופותרים. להלן הפתרון

שאלה 6 
נתונה המשוואה 
 
לפניכם אחד מהשלבים בפתרון של המשוואה:

א. האם השלב המוצג נכון? הסבירו כיצד הוא מתקבל מהמשוואה.
ב. פתרו את המשוואה

פתרון שאלה 6
א. השלב מוצג נכון. תחום ההגדרה של x הוא כמוצג לפי העיקרון כי הביטוי במכנה שונה מ- 0.

לאחר שמוגדר תחום ההגדרה אפשר לפתח המשוואה:

ב. והמשך פתרון עד הסוף


קישורים:

מבחן מפמ"ר מתמטיקה כיתה ט - רמה רגילה תשע"ב - שאלות פתורות: שאלות 1-6 , שאלה 7 , שאלות 8-9 , שאלה 10 , שאלה 11 , שאלות 12-13 , שאלה 14 -15 , שאלה 16

שאלות פתורות ממבחן מיצ"ב לכיתה ח' תשס"ח ב - חלק א

שאלה מספר 1 - פִּתְרוּ את המשוואה, הציגו את דרך הפתרון וּבִדְקוּ את תשובתכם.

 

פתרון:

בדיקה
מציבים  x = 4 במשוואה

 

הבדיקה הצליחה

שאלה מספר 2

סמנו את הגרף המתאר את הפתרון של האי שוויון שלפניכם: 5 > 2x-

 

פתרון

נפתור את אי השוויון

נחלק את שני האגפים ב- (2-) , כיוון האי שוויון מתהפך

נקבל

 התיאור הגרפי המתאים הוא מספר 1

שאלה מספר 3

במבחן ארצי במתמטיקה נבחנו 6,200 תלמידים.

א. 12% מהתלמידים לא השיבו על השאלה האחרונה במבחן.
כמה תלמידים השיבו על השאלה האחרונה במבחן?

הציגו את דרך החישוב.

פתרון סעיף א

נחשב תחילה את מספר התלמידים שלא השיבו על השאלה האחרונה במבחן: 

 

 מספר התלמידים שלא השיבו על השאלה האחרונה במבחן: 744

מספר התלמידים שהשיבו על השאלה האחרונה שווה לסה"כ התלמידים פחות אלו שלא השיבו:

תשובה לסעיף א: 5456


ב. 2.5% מהתלמידים לא השיבו על השאלה הראשונה במבחן.
כמה תלמידים לא השיבו על השאלה הראשונה במבחן?
הציגו את דרך החישוב.
פתרון סעיף ב
2.5% מכל 6,200 התלמידים לא השיבו על השאלה הראשונה: 

תשובה סעיף ב: 155 תלמידים לא השיבו על השאלה הראשונה במבחן.


שאלה מספר 4

על פאותיה של קובייה הוגנת רשומים שישה משמות ימי השבוע:

 

 

ראשון, שני, שלישי, רביעי, חמישי, שישי.
על כל פאה רשום שמו של יום אחר.
איתי מטיל את הקובייה.
חַשְּבוּ מהי ההסתברות שהקובייה תראה שם של יום המתחיל באות "ר".

פתרון שאלה 4
מרחב התוצאות האפשריות מכיל 6 איברים:
 { ראשון, שני, שלישי, רביעי, חמישי, שישי}

התוצאות האפשריות המתחילות באות ר הן שתיים: {ראשון, רביעי}
הקוביה הוגנת כלומר הסתברות שווה לכל תוצאת בהטלה, לכן ההסתברות לתוצאה המתחילה באות ר' הוא 2 (ראשון, רביעי) מתוך שש ( ראשון, שני, שלישי, רביעי, חמישי, שישי)
ולכן  ההסתברות היא 2/6 = 1/3
ההסתבורת שהקובייה תראה שם של יום המתחיל באות "ר" שווה שליש.


שאלה מספר 5

הציגו את דרך החישוב ונמקו כל חישוב בעזרת משפט מתאים.

פתרון שאלה מספר 5 

השיטה: מוצאים את שוית ABD השווה לזווית לזוית BAD (40 מעלות) לפי זוויות בסיס במשולש ADB שווה שוקיים (AD = DB). לאחר מכן מסכמים את זויות משולש ABC ל- 180 מעלות ומוצאים את .

1: - זוויות בסיס במשולש ADB שווה שוקיים (AD = DB) שוות
2: - נתון
3: - נובע מ-1  ו- 2

סכום הזוויות במשולש ABC שווה 180 מעלות לכן:

נציב את ונקבל:

שאלה מספר 6
פִּתְרוּ את מערכת המשוואות שלפניכם באחת משתי הדרכים:
בדרך האלגברית או בדרך הגרפית. הציגו את דרך הפתרון.

פתרון שאלה 6
נפתור את מערכת המשוואות בדרך אלגברית בשיטת ההצבה.

נפתח תחילה את המשוואה הראשונה ונחלץ את y:


נפשט המשוואה השניה ונציב בה: y = 2 - x

פישוט המשוואה השניה:


הצבה  y = 2 - x ופתרון.



תשובה: x = 4 ,   y = -2

לחלק ב השאלות הפתורות הקלק כאן 

קישורים:

• תרגילים פתורים - מתוך מבחן מיצ"ב מתמטיקה כיתה ח' - תשע"א ב' - חלק א 
• תרגילים פתורים - מתוך מבחן מיצ"ב מתמטיקה כיתה ח' - תשע"א ב' - חלק ב