הוכח בדרך האינדוקציה כי מספר האלכסונים D במצולע (קמור) בעל n צלעות הוא: 
הוכחה:
נתחיל מבדיקת הנוסחה עבור מרובע שהוא מצולע בעל מספר צלעות הנמוך ביותר שיש לו אלכסונים.
למרובע 4 צלעות n = 4 ושני אלכסונים D = 2
נבדוק:

הבדיקה הצליחה.
נניח שעבור n = k מספר האלכסונים במצולע הוא :

צריך להוכיח שעבור n = k+1 מספר האלכסונים הוא:
1:
נדמיין מצולע בעל k צלעות ו- k קודקודים בעל D אלכסונים. אם נוסיף קודקוד נוסף נקבל מצולע חדש (בעל k+1 קודקודים, צלעות) עם אותם אלכסונים ועוד k-1 אלכסונים נוספים שנוצרו עקב הקודקוד החדש.
הקודקוד החדש יוצר k-2 אלכסונים חדשים עם קודקודים שאינם סמוכים לו ועוד אלכסון שנוצר מצלע שהפכה לאלכסון.
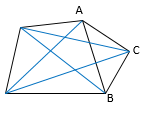
לדוגמא - הוספת קודקוד למרובע והפיכתו למחומש:
המחומש להלן הוא כמו המרובע לעיל בתוספת קודקוד C. נוצרו 2 אלכסונים מחיבור C עם 2 קודקודים שאינם סמוכים ל- C ועוד אלכסון מצלע AB שהפכה לאלכסון סה"כ נוצרו 4-1 = 3 אלכסונים.
לכן מספר האלכסונים במצולע בעל k+1 קודקודים (צלעות):

וזה מה שנדרשנו להוכיח באינדוקציה ב- 1 לעיל.
הוכחה:
נתחיל מבדיקת הנוסחה עבור מרובע שהוא מצולע בעל מספר צלעות הנמוך ביותר שיש לו אלכסונים.
למרובע 4 צלעות n = 4 ושני אלכסונים D = 2
 |
| למרובע שני אלכסונים |
נבדוק:
הבדיקה הצליחה.
נניח שעבור n = k מספר האלכסונים במצולע הוא :
צריך להוכיח שעבור n = k+1 מספר האלכסונים הוא:
1:
נדמיין מצולע בעל k צלעות ו- k קודקודים בעל D אלכסונים. אם נוסיף קודקוד נוסף נקבל מצולע חדש (בעל k+1 קודקודים, צלעות) עם אותם אלכסונים ועוד k-1 אלכסונים נוספים שנוצרו עקב הקודקוד החדש.
הקודקוד החדש יוצר k-2 אלכסונים חדשים עם קודקודים שאינם סמוכים לו ועוד אלכסון שנוצר מצלע שהפכה לאלכסון.
לדוגמא - הוספת קודקוד למרובע והפיכתו למחומש:
המחומש להלן הוא כמו המרובע לעיל בתוספת קודקוד C. נוצרו 2 אלכסונים מחיבור C עם 2 קודקודים שאינם סמוכים ל- C ועוד אלכסון מצלע AB שהפכה לאלכסון סה"כ נוצרו 4-1 = 3 אלכסונים.
לכן מספר האלכסונים במצולע בעל k+1 קודקודים (צלעות):
וזה מה שנדרשנו להוכיח באינדוקציה ב- 1 לעיל.