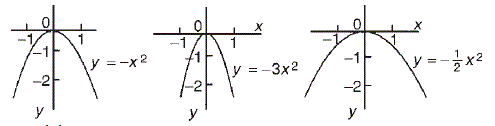מעבר חום ותרמודינמיקה

מעבר חום ותרמודינמיקה 

מעבר חום הוא המדע המבקש לחזות את העברת האנרגיה בחומר כתוצאה מהבדלי טמפרטורה. תרמודינמיקה מלמדת כי העברת אנרגיה זו מוגדרת כחום. מדע מעברת החום מבקש לא רק להסביר כיצד מועברת אנרגיית החום, אלא גם לחזות את הקצב. העובדה שמעבר חום הוא המטרה הרצויה,, מצביעה על ההבדל בין מעבר חום ותרמודינמיקה. תרמודינמיקה עוסקת במערכות בשיווי משקל; בחיזוי כמות האנרגיה הדרושה לשינוי מערכת ממצב אחד לשיווי משקל אחד לאַחֵר; זה לא יכול לשמש כדי לחזות את קצב שבו השינוי יתקיים מאחר והמערכת
לא בשיווי משקל בתהליך. מעבר חום ותרמודינמיקה משלימים אחד את השניה.

כדוגמא לסוגים השונים של בעיות שמטופלות על ידי תרמודינמיקה ומעבר חום, נחשוב על קירור של מוט פלדה חם בדלי מים. בתרמודינמיקה משתמשים כדי לחזות את טמפרטורת שיווי המשקל הסופית של הפלדה והמים. התרמודינמיקה לא תגיד לנו כמה זמן לוקח להגיע למצב שיווי משקל זה, או מה הטמפרטורה של המוט או המים תהיה אחרי אורך מסוים של זמן לפני מצב שיווי המשקל. מעבר חום משמש כדי לחזות את הטמפרטורה של מוט הפלדה והמים כפונקציה של זמן.

ישנם שלושה מונחים של מעבר חום: הולכה, הסעה, וקרינה.

הולכת חום

 
הולכת חום הוא תהליך שבו האנרגיה עוברת דרך מגע ישיר בין חומרים שונים או בתווך של החומר עצמו עקב הפרשי טמפרטורה כאשר זה נכון לכל מצב הצבירה. לדוגמא אם נחזיק מוט ברזל מצידו האחד ביד ונקרבו לאש מצידו השני, החום עובר מקצה המוט הקרוב לאש לשאר המוט עקב הפרשי טמפרטורה.

הסעת חום

הסעת חום היא העברה פיזית של חום, כלומר תנועה של גוף כלשהו שמכיל חום, ממקום אחד למקום אחר. לרוב מתבטאת הסעה בזורמים, כאשר זרם כלשהו של חומר מחליף חומר קר בחומר חם. לדוגמא זרם אויר המקרר רדיאטור, האויר החם בקרבת הרדיאטור מוסע משם ומוחלף באויר אחר וכך מתקרר הרדיאטור.

קרינת חום

 
גופים חמים פולטים קרינה, שגורמת לקירורם, לדוגמא מנורה או מקרן חום, דוגמא נוספת היא השמש הפולטת קרינה ובכך מעבירה חום למרחקים.

קוי שדה חשמלי

בפיסיקה והנדסה ניתן להגדיר סוגים רבים של שדות. השדה הוא תכונה במרחב או מישור. דוגמא לשדה היא התפלגות הטמפרטורות באולם. היינו מוצאים על ידי מדידת הטמפרטורה בנקודות רבות באולם. באופן דומה, אנחנו יכולים להגדיר שדה לחץ מים בבריכה שחייה. שדות כאלה הם דוגמאות של שדות סקלרים כי טמפרטורה ולחץ הם כמויות סקלריות, שיש להם רק גדלים וכיוונים לא.

השדה החשמלי - גודל וכיוון

השדה החשמלי הוא שדה וקטורי כי יש לו גודל וכיוון. כדי לברר בנקודה מסוימת מהו גודל השדה וכיוונו נציב חלקיק בוחן בעל מטען חיובי q0 כלשהו, ונבדוק מהו גודל הכוח המופעל עליו וכיוונו ומזה נגזור את השדה החשמלי.

נניח בנקודה P במרחב ישנו חלקיק טעון חשמלית מטען חיובי q0 ופועל עליו כוח . השדה החשמלי בנקודה P במרחב מוגדר:

 מאחר ומטען הבוחן q0 הוא חיובי הכיוון של השדה החשמלי  הוא אותו הכיוון של הכוח המופעל על מטען הבוחן.
הגודל E של השדה החשמלי הוא E = F/q0

 קוי שדה חשמלי

ניתן לתאר את השדה החשמלי במרחב מסוים ע"י קוים המקבילים לכיווני הכוחות הפועלים על חלקיקי בוחן במרחב. כאשר הקוים צפופים יותר במישור מאונך להם משמעות הדבר היא כי גודל השדה גדול יותר.

קוי שדה חשמלי סביב כדור טעון מטען שלילי

קוי שדה חשמלי סביב פלטה אינסופית עטונה מטען חיובי

מעגל RC עם מקור מתח קבוע

מעגל RC הוא מעגל חשמלי עם נגד R וקבל C. בדוגמא לפנינו יש במעגל גם מקור מתח V  ומתג, והקבל אינו טעון במטען כלשהו בתחילה. בזמן t = 0 המתג עובר ממצב נתק למצב קצר ומתחיל לזרום זרם במעגל המשתנה בזמן. הזרם בזמן t = 0 הוא V/R מאחר וקבל לא טעון מתפקד ברגע t=0 כקצר.

מעגל RC עם מקור מתח ומתג

במעגל RC הקבל נטען באנרגיה בין שתי הפלטות כאשר מחובר אליו המתח. ברגע שהקבל טעון לחלוטין הזרם יורד ל- 0 והקבל מתפקד כנתק.

המתחים על הנגד R והקבל C (המתחים על הקבל והנגד והזרם i משתנים כפונקציה של הזמן t) הם כדלקמן:



ע"פ חוקי קירכהוף סכום המתחים במעגל שווה 0 לכן:

המתח V של מקור המתח קבוע בזמן.

נפתור את המשוואה ע"י הפיכתה למשוואה דיפרנציאלית ע"י גזירה בזמן:


קיבלנו משוואה דיפרנציאלית לינארית מהמעלה הראשונה בעלת פתרון כללי:


כאשר K קבוע ניתן למציאה ע"י הצבת תנאי התחלה.

ברגע t =0 הקבל אינו טעון כלל ולכן משמש כקצר, הזרם במעגל בזמן t=0 הוא V/R.

מהצבת תנאי התחלה מקבלים K = V/R

ולכן הזרם במעגל כפונקציה של הזמן הוא:




נסמן ב-   את קבוע הזמן. קבוע הזמן הוא הזמן הנדרש לטעון את הקבל במלואו בזרם קבוע השווה לזרם ההתחלתי V/R , קבוע הזמן הוא גם הזמן הנדרש לטעון 63.2% מהקבל במעגל עם זרם משתנה ע"פ נוסחת הזרם לעיל.

במעגל RC קבוע הזמן שווה:

גרף הדעיכה של הזרם במעגל יראה כך:

גרף דעיכת זרם במעגל RC

המתחים על הנגד והקבל כפונקציה של הזמן

מהצבת הזרם i במשוואות המתחים על הנגד והקבל נקבל:

משוואות המתחים על הקבל והנגד במעגל RC

למציאת קבוע האינטגרציה במשוואת הקבל משתמשים בתנאי התחלה שהזרם במעגל בזמן t=0 הוא V/R , או שהמתח על הקבל שווה ל- 0  מאחר והקבל אינו טעון כלל בזמן t=0.

גרפי המתחים על הקבל והנגד:

גרפי מתחים על קבל ונגד במעגל RC עם מקור מתח קבוע

פתרון שאלה 5 מבגרות מתמטיקה 3 יחידות קיץ 2015 - הסתברות וסטטיסטיקה

שאלה 5 

 

לכל אדם יש אחד מסוגי הדם האלה: A , B , AB , O

 ל- 40% מהאוכלוסייה (בקירוב) יש סוג דם A.

 ל- 20% מהאוכלוסייה (בקירוב) יש סוג דם B.

 ל- 5% מהאוכלוסייה (בקירוב) יש סוג דם AB.

א. לכמה אחוזים מהאוכלוסייה יש סוג דם O?

ב. בעל סוג דם B יכול לקבל דם מבעל סוג דם O ומבעל סוג דם B בלבד.

    מהי ההסתברות שתורם אקראי יוכל לתרום לבעל סוג דם B?   

ג. בעל סוג דם B יכול לתרום דם לבעל סוג דם AB ולבעל סוג דם B בלבד.

    מהי ההסתברות שתורם בעל סוג דם B יוכל לתרום לאדם אקראי?  

ד. בעל סוג דם O יכול לקבל דם מבעל סוג דם O בלבד.

    מהי ההסתברות שתורם אקראי יוכל לתרום דם לבעל סוג דם O?

ה.  בעל סוג דם O יכול לתרום לכולם.

 מהי ההסתברות שתורם בעל סוג דם O יוכל לתרום לאדם אקראי?

פתרון

 א. ע"פ נתוני השאלה התפלגות סוגי הדם באוכלוסיה היא:

שיעור באוכלוסיה ..... סוג דם
 40% ...................... A
20% ........................ B
5% ......................... AB

מאחר ולכל אדם יש אחד מסוגי דם אלה: A, B, AB, O

שיעור האוכלוסייה עם סוג דם O הוא:

100% - 40% - 20% - 5% = 35%

ל- 35% - מהאוכלוסייה יש סוג דם O.

ב. ל- 35% מהאוכלוסייה יש סוג דם O, ול- 20%  מהאוכלוסייה יש סוג דם B. ההסתברות שתורם אקראי מהאוכלוסייה הוא סוג דם B או O הוא: 35% + 20% = 55%

התשובה היא 55%.

 

ג. בעל סוג דם B יכול לתרום דם רק לבעל סוג דם B או AB.

מכיוון של- 20% + 5% = 25% מהאוכלוסייה יש סוג דם B או AB, ההסתברות היא 25% = 0.25.

תשובה: ההסתברות היא 0.25.

ד. בעל סוג דם O יכול לקבל דם רק מבעל סוג דם O. מכיוון של- 35% מהאוכלוסייה יש סוג דם O, הם יכולים לתרום דם לבעל סוד דם O.

ההסתברות היא: 35% = 0.35.

ה. בעל סוג דם O יכול לתרום לכולם, לכן אם נבחר אדם באקראי בעל סוג דם O יוכל לתרום לו בוודאות. לכן ההסתברות שתורם בעל סוג דם O יוכל לתרום לאדם אקראי היא 100% = 1.

 

פירמידה ישרה שבסיסה מלבן - הנדסת המרחב - מבגרות מתמטיקה 3 יחידות קיץ 2015

שאלה 4

 
הבסיס ABCD של פירמידה ישרה SABCD הוא מלבן. SH הוא גובה הפירמידה (ראה ציור).

נתון (מידות בס"מ):
AD = 16
AB = 26
SH = 28

א. חשב את אורך האלכסון של בסיס הפירמידה.
ב. חשב את האורך של מקצוע צדדי של הפירמידה.
ג. חשב את גודל הזווית שבין מקצוע צדדי ובין בסיס הפירמידה.

 

פתרון שאלה 4

א. נתון כי בסיס הפירמידה ABCD הוא מלבן שצלעותיו AB = 26 , AD = 16  (המידות בס"מ)
לכן BD אלכסון בסיס הפירמידה הוא אלכסון מלבן ABCD ויתר במשולש ABD (אלכסון המלבן מחלק אותו לשני משולשים ישרי זוית).
ע"פ משפט פיחגורס במשולש ישר זוית ABD ריבוע היתר שווה לסכום ריבועי הניצבים:

BD² = AB² + AD² = 26² + 16² = 676 + 256 = 932

BD = √932 = 30.53

אורך אלכסון בסיס הפירמידה הוא 30.53 ס"מ

ב. לחישוב אורך מקצוע צדדי נתבונן במשולש SHB. המשולש ישר זוית משום שנתון כי SH הוא גובה הפירמידה ולכן אנל לכל הישרים במישור ABCD ובתוכם BH.
 נקודה H היא אמצע האלכסון BD מאחר והפירמידה ישרה. לכן BH = BD/2 = 30.53/2 = 15.265
ע"פ משפט פיחגורס במשולש ישר זוית SHB ריבוע היתר שווה לסכום ריבועי הניצבים:

∆ SDH

SD² = SH² +HD²

SD^2 = 28² + 15.26²

SD = √1017

SD = 31.89

אורך המקצוע הצדדי הוא 31.89 ס"מ.

ג. חישוב הזווית שבין מקצוע צדדי ובין בסיס הפירמידה

הפירמידה ישרה ולכן מקצועותיה שווים. בסיס הפירמידה מלבן לכן מטעמי סימטריה כל מקצועותיה יוצרים זויות שוות עם בסיסה. נתייחס אל המקצוע SB.
הזוית בין המקצוע לבסיס היא הזוית בין המקצוע להיטלו על הבסיס. במקרה שלנו ההיטל הוא BH משום ש- SH מאונך לבסיס ויוצר את ההיטל BH.

במשולש SHD

sin∢SDH = SH / SD

sin∢SDH = 28 / 31.89

sin∢SDH = 61.4°

הזווית שבין מקצוע צדדי לבסיס הפירמידה שווה 61.40° .
 

חישובים בטרפז - טריגונומטריה - מבגרות מתמטיקה 3 יחידות קיץ 2015

שאלה מספר 3

 

 בטרפז ABCD  שבו AD||BC   נתון:

22 ס"מ  = AB.

(ראה ציור)

א. חשב את גובה הטרפז.

ב. חשב את אורך השוק DC.

ג. נתון גם: 12 ס"מ = AD.

חשב את אורך הבסיס BC.

פתרון שאלה 3

 
בניית עזר: מורידים אנך מנקודה A ל- BC בנקודה P, ואנך מנקודה D ל- BC בנקודה Q.
נוצר מרובע ADQP שבו צלעות נגדיות מקבילות וצלעות סמוכות מאונכות לכן מרובע ADQP הוא מלבן.

א. גובה הטרפז הוא המרחק בין שני בסיסיו המקבילים כלומר AP. במשולש ABP:

גובה הטרפז הוא 14.14 ס"מ.

ב. מאחר ו- ADQP מלבן אזי AP = DQ = 14.14 , במשולש DQC:


אורך השוק DC הוא 28.28 ס"מ

ג. נחשב את אורך הבסיס הגדול.

 

כיוון שמרובע ADFE הוא מלבן, הרי שגם EF =   ס״מ  12 .

 

אורך הבסיס הגדול הוא: 

16.85 + 12 + 24.49 = 53.34 ס"מ

תשובה: אורך הבסיס הגדול הוא 53.34 ס"מ.

סדרה הנדסית - מבגרות מתמטיקה 3 יחידות קיץ 2015

שאלה מספר 2

 

ההיקפים של משולשים שווי צלעות מהווים סדרה הנדסית עולה (ראה ציור).

בסדרה 8 משולשים.

 

אורך הצלע של המשולש הראשון הוא 3 ס"מ, ואורך הצלע של המשולש השני הוא 6 ס"מ.

א. מהו ההיקף של המשולש השלישי בסדרה?

ב. מהו ההיקף של המשולש האחרון בסדרה?

ג. מהו סכום ההיקפים של שמונת המשולשים?

רקע סדרה הנדסית:

 סדרה הנדסית מוגדרת על ידי שני מרכיבים: האיבר הראשון שלה ומנת איבריה. משני נתונים אלו ניתן לדעת את ערכו של כל איבר בסדרה. אם  הוא האיבר הראשון ו־ q היא מנת הסדרה, האיבר ה־ n-י נתון על ידי הנוסחה:  a_n = a₁ ᐧ q^n-1

ניתן לחשב את סכום הסדרה עד האיבר ה־-י (כולל) בעזרת הנוסחה :  S_n = a₁ ᐧ (qⁿ - 1) / (q - 1)

פתרון שאלה 2

א. היקפי המשולשים מהווים סדרה הנדסית. נחשב תחילה את האיבר הראשון בסדרה a₁ ואת מנת הסדרה q.
אורך צלע המשולש הראשון הוא 3 ס"מ וכל המשולשים שווי צלעות לכן היקף המשולש הראשון הוא 9 ס"מ וזהו גם האיבר הראשון בסדרה a₁ = 9.
אורך צלע המשולש השני הוא 6 ס"מ לכן היקפו הוא 18 ס"מ: a₂ = 18
מנת הסדרה q היא המנה בין מספר בסדרה לקודמו:   

q = a₂ / a₁ = 18 / 9 = 2

לכן מנת הסדרה q = 2
היקף המשולש השלישי בסדרה הוא האיבר השלישי בסדרה ההנדסית:   

a₃ = a₁ ᐧ q² = 9 ᐧ 2² = 36

ב. היקף המשולש האחרון בסדרה הוא האיבר השמיני בסדרה ההנדסית:

a₈ = a₁ ᐧ q⁷ = 9 ᐧ 2⁷ = 1152

ג. סכום ההיקפים של שמונת המשולשים הוא סכום שמונת  האיברים בסדרה ההנדסית:

S₈ = a₁ ᐧ (q⁸ - 1) / (q - 1)

S₈ = 9 ᐧ (2⁸ - 1) / (2 - 1) = 9 ᐧ 255 = 2295

פרבולה - מבגרות מתמטיקה 3 יחידות קיץ 2015

שאלה מספר 1

 

בסרטוטים שלפניך מוצגים שני גרפים, (1) ו- (2), 

של הפונקציות:  f(x)= x² - 6x

                         g(x) = -x² +5x +6

 

א. מבין הגרפים , (1) ו- (2) , איזה גרף הוא של הפונקציה f(x) , ואיזה גרף הוא של הפונקציה g(x)? נמק.

ב.שני הגרפים נחתכים בנקודות B ו- D, כמתואר בציור.

מצא את השיעורים של הנקודה B ואת השיעורים של הנקודה D.

ג. עבור אילו ערכים של x גרף (2) נמצא מעל גרף (1)?

 

פתרון שאלה מספר 1

 1. לפונקציה ריבועית מהצורה   y = aᐧx² + bᐧx + c  (פרבולה) יש נקודת מינימום כאשר a > 0 ונקודת מקסימום כאשר a <0 .

לפונקציה  f(x) = x² - 6ᐧx  פרמטר a = 1 כלומר a > 0 ולכן לפונקציה נקודת מינימום. מכאן הגרף המתאים לפונקציה f הוא גרף מספר 1.

2.למציאת נקודות חיתוך בין שתי הפונקציות, נשווה ביניהן ונפתור את המשוואה המתקבלת:

f(x) = x² - 6x

g(x) = -x²  + 5x + 6

f(x) = g(x)

x² - 6x = -x²  + 5x + 6

2x² - 11x - 5 = 0

למשוואה ריבועית (משוואה ממעלה שניה) מהצורה:   y = aᐧx² + bᐧx + c

יש שני שורשים:


נפתור


נמצא את שיעורי y - עבור x1 = 6:

f(x) = x² - 6ᐧx

f(x1 = 6) = 6² - 6ᐧ6 - 36 - 36 = 0

נמצא את שיעורי y - עבור x2 = -0.5:

f(x2 = -0.5) = (-0.5)^2 - 6 * (-0.5) = 3.25

שיעורי הנקודות B, D:  


3. גרף 2 נמצא מעל גרף 1 בין הנקודות B ו- D כלומר עבור x:  

גרפים של פרבולות - חלק ב

לצפיה בגרפים של פרבולות חלק א הקלק כאן

 נבחן את הפונקציה הריבועית מהצורה   y = aᐧx² + c
 a, c הם פרמטרים, ו- x, y הם הפונקציה והארגומנט.

 נבחן את הפונקציות הריבועיות הבאות:

y = x² + 3

y = x² - 2

y = -x² + 2

y = -2ᐧx² - 1

 להלן הגרפים של הפונקציות

 

גרפים של פרבולות עם נקודות מינימום / מקסימום, ועם / ללא נקודות חיתוך עם הצירים

לסיכום, כאשר    y = aᐧx² + c

1. הפרבולה סימטרית ביחס לציר y (וקדקודה על ציר y)
2. גודלו של a משפיע על הגרדיאנט של הגרף (שינוי הגרף ביחס ל- x, רוחב הפרבולה), ככל ש- a  גדול יותר הפרבולה רחבה יותר.
3. הקבוע c הוא נקודת חיתוך הפרבולה עם ציר y.
4.  כאשר a חיובי לפרבולה נקודת מינימום, וכאשר a שלילי לפרבולה נקודת מקסימום.

גרפים של פרבולות - חלק א

נבחן את הפונקציה הריבועית מהצורה  y = aᐧx²
a הוא פרמטר, ו- x, y הם הפונקציה והארגומט

נתחיל כאשר a > 0 ונבחן 3 פונקציות:

 y = x²

 y = 3x²

 y = ½ᐧx²

הגרפים יראו כך:

גרפים של פרבולות עבור a > 0

נבדוק עבור a < 0  ונבחן את שלשת הפונקציות:

 y = -x²

 y = -3x²

 y = -½ᐧx²

הגרפים יראו כך:

גרפים של פרבולות עבור a < 0

נוכל לסכם עבור y = aᐧx² :   

א. קודקוד הפרבולה נמצא בראשית הצירים.
ב. הפרבולה סימטרית ביחס לציר y
ג. גודלו של a משפיע על הגרדיאנט של הגרף (שינוי הגרף ביחס ל- x, רוחב הפרבולה), ככל ש- a  גדול יותר הפרבולה רחבה יותר.
ד. כאשר a חיובי לפרבולה נקודת מינימום, וכאשר a שלילי לפרבולה נקודת מקסימום.

לצפיה בגרפים של פרבולות חלק ב הקלק כאן

דלתון חסום במלבן - גיאומטריה - ממבחן מפמ"ר לכיתה ט רמה רגילה - תשע"ד

שאלה 5 - גיאומטריה - ממבחן מפמ"ר לכיתה ט רמה רגילה - תשע"ד

נתון: המרובעים ABCD ו- PLCD הם מלבנים. הנקודה K היא אמצע הצלע AB. הנקודה M היא אמצע הצלע DC.
O היא נקודת המפגש של אלכסוני המרובע KLMP 

א. הוכיחו: המרובע KLMP הוא דלתון.

ב. נתון גם   KO = PL / 2.

הוכיחו: AKOP הוא ריבוע.

ג. נתון גם:   PK = √2  יחידות.
   
הנקודה P מחלקת את הצלע AD כך ש:  AP:PD = 1:3.
חשבו את שטח המלבן ABCD.


פתרון

א.  נוכיח שהמרובע KLMP הוא דלתון ע"י הוכחת שוויון הצלעות הסמוכות: KL = KP, MP = ML

נוכיח חפיפת משולשים: KBL, KAP

1: AK=BK  - נתון - (הנקודה K היא אמצע הצלע AB)
2: - זויות המלבן ABCD שוות 90 מעלות ושוות ביניהן.

 CL = DP - צלעות נגדיות במלבן PLCD שוות
 AD = BC -  צלעות נגדיות במלבן ABCD שוות

3: BC - CL = AD - DP   - הפרשים בין גדלים שווים
4: BL = BC - CL - נתון
5: AP = AD - DP  - נתון

6:  AP = BL - נובע מ- 3,4,5

     - נובע מ- 1,2,6 - צ.ז.צ
7: מהחפיפה נובע: KL = KP

8:   בדרך דומה מוכיחים שיוויון צלעות ML = MP ע"י חפיפת משולשים  MCL, MDP

מהשיוויונות KL = KP ו- ML = MP נובע כי המרובע KLMP הוא דלתון. ( מרובע שיש לו שני זוגות נפרדים של צלעות סמוכות השוות זו לזו, הוא דלתון)

ב. נוכיח כי מרובע AKOP הוא ריבוע ע"י שיוויון בין צלעות סמוכות ושיוויון זויות המרובע ל- 90 מעלות
הוכחה
1: PO =OL - האלכסון הראשי בדלתון מאונך לאלכסון המשני וחוצה אותו  - דלתון KPML , אלכסון ראשי KM, אלכסון משני PL
2:      - האלכסון הראשי בדלתון מאונך לאלכסון המשני וחוצה אותו  - דלתון KPML , אלכסון ראשי KM, אלכסון משני PL

3: AK ||PO - שתי הצלעות מקבילות לצלע CD (מאחר ומרובעים ABCD, PLCD מלבנים)
4: באותה דרך מוכיחים KO||AP

מרובע  AKOP ריבוע - נובע מ- 1,2,3,4 - מרובע ששתי זוגות צלעות נגדיות מקבילות, זוג צלעות סמוכות שוות והזוית ביניהן ישרה  ריבוע עקב שוויון כל צלעותיו וזויותיו.

מבחן מיצ"ב מתמטיקה כיתה ח - מאי 2014 - שאלות 19-21 ופתרונן

להלן פתרון לשאלות 19-21 מבחן מיצ"ב מתמטיקה כיתה ח שנערך במאי 2014.
להורדת המבחן בקובץ PDF הקלק כאן

שאלה 19

אלעד מעוניין לשלוח חבילה. הוא בדק מחירים בשתי חברות משלוחים:

(1) חברת "איילה" גובה תשלום התחלתי ותשלום בעבור משקל החבילה בק"ג.
(2) חברת "הצבי" אינה גובה תשלום התחלתי, אך גובה תשלום בעבור משקל החבילה בק"ג.
הגרפים שלפניכם מתארים את המחירים בש"ח (y) כפונקציה של משקל החבילה בק"ג (x) בכל אחת מחברות המשלוחים.

א. מהו משקל החבילה (בק"ג) שבעבורו יהיה המחיר בחברת “הצבי" שווה למחיר בחברת “איילה"?

ב. סַמנו את הפונקציה המתארת את המחיר בש"ח (y) כפונקציה של משקל החבילה בק"ג (x) בחברת   “הצבי".
y = x .1
y = 3x .2
y = 10x .3
y = 15x .4

ג. גם חברת "יונה" גובה תשלום התחלתי ותשלום בעבור משקל החבילה בק"ג. אלעד בדק מחירים גם בחברת "יונה" ומצא שלא משנה מה יהיה משקל החבילה, המחיר שישלם לחברת "יונה" יהיה גבוה יותר מהמחיר שישלם לכל אחת משתי החברות האחרות.

כִּתבו דוגמה לפונקציה קווית המתארת את המחיר בש"ח (y) כפונקציה של משקל החבילה בק"ג (x) בחברת “יונה".

פתרון

א. ניתן לראות כי הגרפים של חברות "הצבי" ו"איילה" מציגים ערך מחיר (הגרפים נחתכים) זהה כאשר משקל החבילה הוא 4 ק"ג.

ב. ניתן לראות בגרף חברת שכאשר משרל החבילה 1 ק"ג, המחיר 15 ש"ח, עבור משקל 2 ק"ג המחיר 30 ש"ח, לכן קשר המחיר בש"ח (y) כפונקציה של משקל החבילה בק"ג (x) בחברת   “הצבי" הוא  y = 15x, כלומר תשובה 4 היא הנכונה.

ג. כדי שהמחיר של חברת "היונה" יהיה תמיד יותר גבוה נציב 2 דרישות. נקודת חיתוך עם ציר y גדולה מ- 20 וזה כדי שמחיר התחלתי של חברת היונה יהיה גבוה מחברת "איילה", וכן נדרוש ששיפוע הפונקציה הקוית יהיה גדול מ- 15 כדי שמחיר לק"ג של חברת "היונה" יהיה גבוה מחברת "הצבי".
לפיכך אם הפונקציה קווית המתארת את המחיר בש"ח (y) כפונקציה של משקל החבילה בק"ג (x) בחברת “יונה", הוא מהצורה: y = ax +b
נדרוש ש: b>20 , a>15
דוגמאות:
y = 20x +25
y = 30x +40

להלן דוגמא לגרף חברת "היונה"  y = 20x +25

דוגמא לגרף חברת "היונה"  y = 20x +25

שאלה 20
למשפחת מרום טלוויזיה מלבנית המורכבת ממסך וממסגרת, כפי שמתואר בסרטוט שלפניכם .
המסך בסרטוט צבוע בלבן, והמסגרת צבועה באפור.
גודל המסך הוא 25 אינצ'ים. גודל המסך נקבע על פי אורך אלכסונו (ללא המסגרת)

המידות בסרטוט הן באינצ'ים.
א . x מייצג את הצלע הקצרה של המסך. על פי הנתונים שבסרטוט חַשבו את x (באינצ'ים). הַציגו את דרך הפתרון

 ב . מהו שטח המסגרת הצבועה באפור (באינצ'ים ריבועיים)? הַציגו את דרך הפתרון.

ג . מרחק הישיבה המומלץ לצפייה בטלוויזיה גדול פי– 3 מגודל מסך הטלוויזיה (אלכסון המסך).
נתון: 2.54 ס"מ = 1 אינץ'.
באיזה מרחק מהמסך במטרים מומלץ למשפחת מרום לצפות בטלוויזיה?
הַציגו את דרך הפתרון.

 א.  צורת מסך הטלביזיה היא מלבן שאלכסונו מחלק אותו לשני משולשים ישרי זוית, כאשר האלכסון הוא היתר וצלעות המסך הן הניצבים. אורך האלכסון הוא 25 אינטש ואורך ניצב אחד הוא 20 אינטש. ניתן למצוא אורך ניצב שני (צלע קצרה של המסך - x) באמצעות משפט פיתגורס:
 

 אורך הצלע הקצרה של המסך הוא 15 אינטש

ב. שטח המסגרת הצבועה באפור שווה לשטח מלבן חיצוני (מסגרת + מסך) פחות שטח מלבן פנימי (מסך).
צלעות המלבן הפנימי הינן: 20x15 . ע"פ השרטוט צלעות המלבן החיצוני גדולות ב- 8 אינטש כל אחת מצלעות המלבן הפנימי. לכן צלעות מלבן חיצוני: 28x23 אינטש.
שטח המסגרת הוא הפרש השטחים:
s = 23*28 - 15*20 = 344
שטח המסגרת הוא 344 אינטש בריבוע.

ג. נחשב תחילה את מרחק הישיבה המומלץ באינטשים ואח"כ נמיר למטרים.
מרחק הישיבה המומלץ לצפייה בטלוויזיה גדול פי– 3 מגודל מסך הטלוויזיה (אלכסון המסך השווה ל- 25 אינטש). לכן המרחק שווה: 3 * 25 = 75 אינטש.
באינטש  אחד יש 2.54 לכן ב- 75 אינטש יש: 75 * 2.54 = 190.5 ס"מ = 1.905 מטר.
המרחק המומלץ למשפחת מרום לצפות בטלוויזיה הוא 1.905 מטר



שאלה 21 - מעגל במערכת צירים
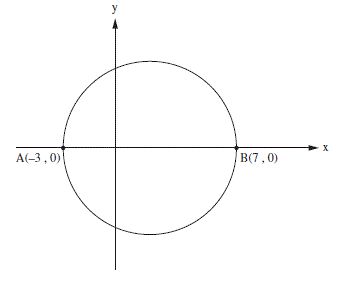
לפניכם מערכת צירים שבה מסורטט מעגל. AB הוא קוטר המעגל.

א . מהו האורך של רדיוס המעגל ביחידות אורך?
1. 10
2. 7
3. 5
4. 4

ב . מהו היקף המעגל ביחידות אורך?

 פתרון

א. AB הוא קוטר המעגל. אורכו של AB הוא המרחק בין נקודה A לנקודה B. מאחר ו- AB הוא קטע אופקי המרחק שווה למרחק בין שיעורי x של נקודות A, B:
 
קוטר המעגל הוא 10 יחידות ולכן רדיוסו 5 יחידות. תשובה 3 היא הנכונה.

ב. היקף P של המעגל שווה:

היקף המעגל הוא 31.42 יחידות

מבחן מיצ"ב מתמטיקה כיתה ח - מאי 2014 - שאלות 16-18 ופתרונן

 להלן פתרון לשאלות 16-18 מבחן מיצ"ב מתמטיקה כיתה ח שנערך במאי 2014.
להורדת המבחן בקובץ PDF הקלק כאן

שאלה 16 - פונקציה לינארית

לפניכם גרף של פונקציה קווית שעליו מסומנות הנקודות .A, B
א . מהי משוואת הישר AB ? הַציגו את דרך הפתרון.
ב . מהו התחום שבו הפונקציה חיובית?

גרף של פונקציה קווית שעליו מסומנות הנקודות .A, B

פתרון:

א. למציאת משוואת פונקציה קוית (פונקציה לינארית), נמצא תחילה את שיפוע הישר ע"פ שתי הנקודות דרכן הוא עובר, ואח"כ נמצא את משוואת ישר במערכת צירים ע"פ שיפוע ונקודה דרכה עובר

מציאת שיפוע הישר AB
 בנוסחה למציאת שיפוע m של ישר העובר דרך שתי נקודות
השיפוע m נתון בנוסחה: 

לכן שיפוע הישר AB :   

מציאת משוואת הישר AB ע"פ השיפוע 3- והנקודה (5,0) דרכה הוא עובר
משוואת הישר בעל שיפוע m העובר דרך נקודה     היא:  
 
משוואת AB הישר:   y= -3x +15

ב. הפונקציה חיובית כאשר y >0 או כאשר הגרף מעל ציר x. ניתן לראות שהתחום הוא כאשר x<5

שאלה 17 - בעיה כללית

מחיר עט יקר ב– 10 ש"ח ממחיר מחברת.
אייל קנה 15 עטים ו– 25 מחברות.
הסכום ששילם אייל בעבור כל העטים היה גדול פי– 3 מהסכום ששילם בעבור כל המחברות.
מהו מחירה של מחברת?
הַציגו את דרך הפתרון.

פתרון

נציב x - מחיר מחברת (בש"ח), מחיר עט יקר ב- 10 ש"ח ממחיר מחברת,
לכן x + 10 - מחיר עט (בש"ח)

מחיר 15 עטים: 
מחיר 25 מחברות: 25x

הסכום ששילם אייל בעבור כל העטים היה גדול פי– 3 מהסכום ששילם בעבור כל המחברות:
 
נפתור את המשוואה כדי למצוא את  x - מחיר מחברת:



מחירה של מחברת הוא 2.5 ש"ח.

שאלה 18

על מערכת הצירים שלפניכם מסומנות נקודות.

נקודות A M P T Q על מערכת צירים

 

ישר מסוים עובר דרך הנקודה ( A(0,–6 והשיפוע שלו הוא 2 . איזו נקודה מהנקודות שלפניכם נמצאת על הישר?
T .1
M .2
Q .3
P .4

 

פתרון:
התשובה הנכונה היא מספר 4 - נקודה P.
שיפוע הישר הוא 2 - מספר חיובי,  לכן מדובר בפונקציה קוית עולה, לכן האפשרויות מצטמצמות לנקודות P, M.
מאחר והשיפוע הוא 2, קצב העליה של y גדול פי 2 מזה של x, מכאן הנקודה המתאימה היא P. נקודה M מתאימה לשיפוע 1.

פפונקציה קוית עולה - שיפוע 2