פתרון שאלה מספר 4 - בגרות 4 יחידות מתמטיקה חורף 2022 - גיאומטריה, מעגל ומשיק ודמיון משולשים

מבחן בגרות מתמטיקה 4 יחידות חורף 2022 - שאלון ראשון

שאלה מספר 4

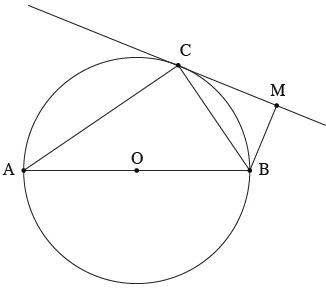
בסרטוט שלפניך מתואר מעגל שמרכזו בנקודה  O.

AB הוא קוטר במעגל.

דרך הנקודה C שעל המעגל, העבירו משיק למעגל.

מן הנקודה B העבירו אנך למשיק, החותך אותו בנקודה  M, ;כמתואר בסרטוט.

א. הוכח:

ב. הוכח:

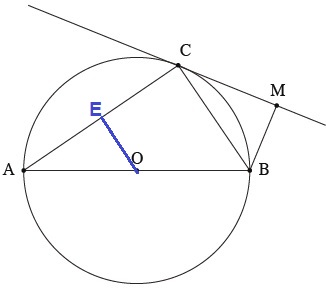
דרך מרכז המעגל, O , העבירו ישר מקביל ל־ BC.

ישר זה חותך את AC בנקודה E.

נתון: שטח המשולש ABC גדול פי 3.24 משטח המשולש CBM ,

OE = 5.  

ג. מצא את AB.

 פתרון שאלה מספר 5

 

א.  הוכח זווית BAC = זווית BCM

השיטה : משולשים BCA CMB ישרי זווית והזוויות בהן שוות מאחר וזווית (חדה) BCM שווה לזווית BAC (זווית היקפית במעגל שווה לזווית בין משיק למיתר עליה היא נשענת).

 נתבונן במשולשים CMB BCA.

1.משולש BCM ישר זווית - זווית BMC ישרה , נתון.

2.משולש BCA ישר זווית - זווית BCA נשענת על קוטר AB (נתון) ולכן ישרה.

3. זווית BAC = זווית BCM - זווית היקפית (BAC) במעגל (O) שווה לזווית בין משיק (CM , נתון) למיתר עליה היא נשענת (BC).

4. זווית CBA = זווית MBC  - נובע מ- 1,2,3 (משלימות ל 90 מעלות במשולשים BCA CMB).

 

 ב. הוכח :  BC*BC = AB*BM

5. מ- 1,2,3,4 נובע כי משולשים CMB, BCA דומים - משולשים ישרי זווית שזוויותיהן החדות שוות.

6. מהדמיון נובע:  BM/BC = BC/AB ולכן BC*BC = AB*BM 

 ג. מצא את AB

 נוכיח כי OE (נתון שווה 5) קטע אמצעים במשולש ABC ןלכן שווה למחצית BC , לכן BC = 10. מאחר ומשולשים CMB, BCA דומים, ויחס השטחים שלהם הוא 3.24 אזי יחס צלעותיהם הוא שורש 3.24 כלומר 8. 

מכאן נסיק שהיחס בין צלע AB ל- BC הוא 1.8 ולכן אורך צלע AB הוא 18.

דרך מרכז המעגל, O , נעביר ישר מקביל ל־ BC, על פי השאלה. ישר זה חותך את AC בנקודה E.

7. OE||BC - נתון

8. AO = BO - נתון , רדיוסים על הקוטר AB

9. OE קטע אמצעים במשולש ABC - נובע מ- 7,8 , על פי משפט הפוך קטע אמצעים.

10. BC = 2OE = 10  - קטע אמצעים OE במשולש ABC שווה למחצית הצלע BC אליה הוא מקביל.

11. משולשים CBM, ABC דומים - הוכח ב- 5

12. שטח המשולש ABC גדול פי 3.24 משטח המשולש CBM 

13. היחס בין צלע AB (במשולש ABC) ל- BC (במשולש CBM) הוא 1.8 - נובע מ- 11, 12 , יחס צלעות במשולשים דומים הוא שורש יחס השטחים.

14. AB = 18 נובע מ- 10, 13

מ.ש.ל
 

מעגל, משיק ומשולש - בגרות 4 יחידות מתמטיקה חורף 2022

מבחן בגרות מתמטיקה 4 יחידות חורף 2022 - שאלון ראשון

שאלה מספר 2

הנקודה M היא מרכז המעגל שמשוואתו

(x - 4)² + (y-3)² = 10

הישר y=2x חותך את המעגל בנקודות A ו־ B , כמתואר בסרטוט שלפניך.

א. מצא את שיעורי הנקודות A ו־  B.

הישר AM חותך את ציר ה־ x בנקודה D (ראה סרטוט).

ב. מצא את שיעורי הנקודה D.

ג. הוכח כי BM מאונך ל־  DM.

ד. האם הישר DB משיק למעגל? נמק.

ה. חשב את שטח המשולש ABD.

 פתרון שאלה 2

א. שיעורי הנקודות A ו - B.

הנקודות A, B הן נקודות חיתוך של מעגל M והישר y = 2x. לכן הנקודות A, B הן פתרון המשוואות המעגל M והישר y = 2x.

נפתור:

(x - 4)² + (y - 3)² = 10

y = 2x

נציב y = 2x במשוואת המעגל ונפתור:

(x - 4)² + (2x - 3)² = 10

x² - 8x + 16 + 4x² - 12x + 9 =10

5x² - 20x + 25 = 10

5ᐧx² - 20x + 15 = 0

x² - 4x + 3 = 0

(x - 1)(x - 3) = 0

קיבלנו 2 שורשים : x1 = 3 , x2 = 1

מאחר ו- y = 2x , נציב ונקבל: y1 = 6 , y2 = 2 .

לכן שיעור הנקודה A הוא: (2, 1)

שיעור הנקודה B הוא: (6, 3)

 

ב. שיעורי הנקודה D.

הנקודה D היא נקודת חיתוך הישר העובר דרך הנקודות M, A עם ציר x.

שיעור הנקודה A חושב בסעיף א : (2 , 1)

ע"פ משוואת המעגל  M :

(x - 4)² + (y - 3)² = 10

שיעור מרכז המעקגל הנקודה M הוא: (3 , 4)

לכן משוואת הישר העובר דרך הנקודות A, M : 

 

משוואת הישר העובר דרך הנקודות M, A היא  3y = x+5.

נקודת חיתוך D של ישר זה עם ציר x היא כאשר  y=0 כלומר:

x + 5 = 0

x = -5

שיעור נקודה D הוא (0 , 5-).

 

 

ג. הוכח כי BM מאונך ל־  DM.

 נחשב שיפוע כל אחד מהקטעים BM, DM, ונבדוק אם הם מקיימים את יחס המאונכות, כלומר מכפלת השיפועים שווה 1-.

נשתמש בנוסחה למציאת שיפוע m של ישר העובר דרך שתי נקודות

השיפוע m נתון בנוסחה: 

שיפוע BM 

שיעור הנקודה B הוא: (6, 3).  חושב בסעיף א.

שיעור M מרכז המעגל שמשוואתו

  (x - 4)² + (y - 3)² = 10  

נובע מידית מהמשוואה.

שיעור הנקודה M הוא  (3 , 4).

 שיפוע BM  הוא :

  (3-4)/(6-3) = 3-

שיפוע DM 

שיעור הנקודה M הוא  (3 , 4).  חושב בסעיף ג.

שיעור נקודה D הוא (0 , 5-). חושב בסעיף ב.

שיפוע DM הוא:   (4+5)/(3-0) = 1/3

שיפועי הקטעים DM, BM מקיימים את יחס המאונכות הואיל ומכפלתם היא 1- = (3-)*1/3

לכן הקטעים DM, BM מאונכים.

ד. האם הישר DB משיק למעגל? נמק.

נשתמש במשפט מאונכות הרדיוס למשיק למעגל בנקודת ההשקה ונבדוק האם הישר DB מאונך לרדיוס MB בנקודת מפגש על המעגל. בדיקת המאונכות תעשה על ידי בדיקת יחס השיפועים. כלומר אם מכפלת שיפוע הישר DB ברדיוס MB שווה 1- אזי DB מאונך לרדיוס MB ולכן DB משיק למעגל.

שיעורי הנקודות M, B , D.

שיעור הנקודה M הוא  (3 , 4). חושב בסעיף ג.

שיעור הנקודה B הוא: (6, 3).  חושב בסעיף א.

שיעור נקודה D הוא (0 , 5-). חושב בסעיף ב.4

חישוב שיפועי  BD, DM:

 שיפוע BM : 

(4-3) / (3-6) = 3-

 שיפוע DB:

(3+5)/(6-0) = 3/4

מכפלת שיפועי BM, DB:

(3-) * (3/4) = 4 / 9- = 2.25- שונה מ- 1-, לכן DB, BM אינם מאונכים והישר DB אינו משיק למעגל M.

ה. שטח המשולש ABD

 למציאת שטח משולש ABD, נבנה בניות עזר את הקטעים BM, AD.

נחשב את שטח המשולש ABD כהפרש שטחי המשולשים MBD, ABM. נוכל להעזר בתכונה שהם משולשים ישרי זוית כפי שהוכחנו בסעיף ג שקטע BM מאונך ל DM.

שטח משולש ABM:

משולש ABM הוא ישר זוית (זוית M) כפי שהוכח בסעיף ג.

ניצבי המשולש ABM הם רדיוסים של המעגל M. והם מאונכים בנקודה M.

אורך הניצבים AM, BM הוא . על פי נוסחת משוואת המעגל: 

(x - 4)² + (y - 3)² = 10

לכן שטח המשולש ABM הוא AMᐧBM/2 = 10 / 2 = 5

 שטח משולש BDM

נמצא את אורכו של MD. שיעור נקודה D הוא (0 , 5- ) , ושיעור נקודה M הוא: (3 , 4) . 

על פי נוסחת מרחק בין שתי נקודות במערכת צירים, המרחק d בין הנקודות M, D:

 אורך DM הוא:

 אורך BM הוא רדיוס המעגל שווה .

משולש BDM הוא ישר זווית מאחר וזווית M ישרה (הוכח סעיף ג).

לכן שטח S משולש BDM:

 שטח משולש ABD הוא הפרש שטחי המשולשים MBD, ABM. לכן שטחו: 15-5 = 10

 שטח משולש ABD הוא 10.

 

הסתברות וסטטיסטיקה - בגרות מתמטיקה 4 יחידות חורף 2022

 מבחן בגרות מתמטיקה 4 יחידות חורף 2022 - שאלון ראשון

 

שאלה מספר 3

במרכז הקהילתי יש שני חוגים בלבד: חוג כדורגל וחוג טניס. אפשר להשתתף בחוג אחד בלבד מבין שני החוגים האלה.

סך כל הבנים המשתתפים בשני החוגים האלה זהה לסך כל הבנות המשתתפות בהם.

80% מן הבנים משתתפים בחוג כדורגל.

מספר הבנות המשתתפות בחוג טניס גדול פי 3 ממספר הבנות המשתתפות בחוג כדורגל.

בוחרים באקראי משתתף בחוגים (בן או בת).

א. מהי ההסתברות שנבחר בן המשתתף בחוג כדורגל?

ב. אם ידוע שנבחר משתתף בחוג טניס, מהי ההסתברות שנבחר בן?

ידוע כי בשני החוגים במרכז הקהילתי יש 200 משתתפים (בנים ובנות) סך הכול.

ג. (1) כמה משתתפים סך הכול (בנים ובנות) יש בחוג טניס?

 (2) מבין כל המשתתפים בחוגים (בנים ובנות) בוחרים באקראי שניים בזה אחר זה (ללא החזרה).

מהי ההסתברות ששניהם משתתפים בחוג טניס?

דייק 3 ספרות אחרי הנקודה העשרונית.

 

פתרון שאלה מספר 3

 

נסמן ב- x את סך כל הבנים המשתתפים בשני החוגים. לכן גם סך כל הבנות בשני החוגים הוא x.

נרשום טבלה של הבנים והבנות המשתתפים בחוג כדורגל ובחוג טניס.

	כדורגל	טניס	סך הכל
בנים	0.8x	0.2x	x
בנות	0.25x	0.75x	x
סך הכל	1.05x	0.95x	2x

א. ההסתברות שנבחר בן המשתתף בחוג כדורגל

סך הבנים המשתתפים בכדורגל הוא 0.8x. סך הבנים והבנות המשתתפים בכדורגל וטניס הוא 2x.

לכן ההסתברות לבחור בן המשתתף בחוג כדורגל הוא 0.8x/2x = 0.4

 

ב. אם ידוע שנבחר משתתף בחוג טניס, מהי ההסתברות שנבחר בן?

 נסמן ב- B מאורע שנבחר משתתף בחוג טניס.

נסמן ב- A מאורע שנבחר בן.

נדרש למצוא את P(A|B) כלומר ההסתברות שנבחר בן בהינתן שנבחר משתתף בחוג טניס.

ידוע נוסחת הסתברות מותנה:

P(A | B) = P(A∩B) / P(B)

 P(A∩B) היא ההסתברות שמאורעות A, B יתקיימו וזה למעשה ההסתברות לבחור בן משחק טניס, לכן:

 P(A∩B) = 0.2x / 2x = 0.1

P(B) היא ההסתברות שנבחר משתתף בחוג טניס: P(B) = 0.95x / 2x = 0.475

לכן ההסתברות ההסתברות  P(A|B) שנבחר בן בהינתן שנבחר משתתף בחוג טניס היא:

P(A|B) =  P(A∩B) / P(B) = 0.1 / 0.475 = 4 / 19 = 0.21052..

ג. סך הכל 200 משתתפים בנים ובנות. לכן יש 100 בנים משתתפים ו- 100 בנות משתתפות.

לכן x = 100. נרשום את הטבלה לעיל ונציב x = 100 .

	כדורגל	טניס	סך הכל
בנים	80	20	100
בנות	25	75	100
סך הכל	105	95	200

(1) בחוג טניס משתתפים סך הכל 95 בנים ובנות.

(2) . מבין כל המשתתפים בחוגים (בנים ובנות) בוחרים באקראי שניים בזה אחר זה (ללא החזרה). מהי ההסתברות ששניהם משתתפים בחוג טניס?

 בחוג הטניס יש 95 משתתפים.

סך כל המשתתפים בחוגים הוא 200.

מרחב המדגם הוא מספר הצירופים של בחירת 2 משתתפים מתוך 200 ללא החזרה וכשהסדר קובע:  

200! / (200 - 2)! = 200 ᐧ 199 = 39,800

 קבוצת ההצלחות הוא מספר הצירופים של בחירת 2 מתוך 95 משתתפי הטניס כשהסדר קובע:

95! / (95 - 2)! = 95 ᐧ 94 = 8,930

ההסתברות שמבין כל המשתתפים בחוגים (בנים ובנות) בוחרים באקראי שניים בזה אחר זה (ללא החזרה), ששניהם משתתפים בחוג טניס, היא:

39,800 / 8,930 = 0.224

בעיית מהירות - מבגרות מתמטיקה 4 יחידות חורף 2022

 מבחן בגרות מתמטיקה 4 יחידות חורף 2022 - שאלון ראשון

 שאלה 1

1 . אורי ודוד רצו לאורך מסלול ישר AB . כל אחד מהם רץ במהירות קבועה.
ביום ראשון הם התחילו לרוץ יחד מאמצע המסלול AB:

אורי רץ מאמצע המסלול לנקודה B , ואילו דוד רץ מאמצע המסלול לנקודה A.

אורי הגיע לנקודה B אחרי 40 דקות, ודוד הגיע לנקודה A אחרי שעה.

נסמן ב־ x את המהירות של דוד (בקמ"ש).

א. הבע את המהירות של אורי באמצעות . x

ביום שני הם התחילו לרוץ יחד מנקודה C הנמצאת על המסלול AB:

אורי רץ מן הנקודה C לנקודה B , ואילו דוד רץ מן הנקודה C לנקודה A.

אורך AC הוא 4.5 ק"מ.

אורי הגיע לנקודה B חצי שעה אחרי שדוד הגיע לנקודה A.

כל אחד מהם רץ באותה המהירות שבה הוא רץ ביום ראשון.

ב. מצא את אורך המסלול AB.

פתרון שאלה 1

א. מהירותו של אורי.

תחילה נבדוק את המרחקים הזהים שעברו דוד ואורי השווים למחצית AB.

מהירותו של דוד היא x (נתון) והוא רץ במשך 1 שעה מאמצע המסלול לנקודה A.

 לכן המרחק שעבר הוא: 1*x = x. מכאן שאורך המסלול AB הוא 2x.

זהו גם המרחק שעבר אורי מאמצע המסלול לנקודה B במשך 40 דקות (או 40/60 שעה = 2/3 שעה).

מכאן שאורי עבר מרחק x (ק"מ) במשך 2/3 שעה. לכן מהירות של אורי היא:

 x/(2/3) = 3x/2 = 1.5x

מהירותו של אורי היא 1.5x .

ב. אורך המסלול AB

מנתוני סעיף א , אורך המסלול AB הוא 2x. 

הנתונים בסעיף א ו-ב מופיעים בטבלה להלן.

	מהירות	דרך	זמן
דוד	x	4.5	4.5/x
אורי	1.5x	2x - 4.5	(2x-4.5)/1.5x

על פי נתוני סעיף ב: "אורי הגיע לנקודה B חצי שעה אחרי שדוד הגיע לנקודה A".

כלומר: 

 (2x - 4.5) / (1.5x) - 4.5/x = 1/2

נפתור ונמצא את x:

(2x-4.5)/1.5  - 4.5 = x/2

נכפיל האגפים ב - 3:

3(2x - 4.5)/1.5  - 3*4.5 = 3x/2

2(2x - 4.5) - 13.5 = 1.5x

4x - 9 - 13.5 = 1.5x

2.5x = 22.5

x =  9

אורך המסלול AB הוא 2x , לכן אורך המסלול AB הוא 18.

חקירת פונקציה היפרבולית - מבגרות מתמטיקה 4 יחידות קיץ 2016

 מתוך מבחן בגרות מתמטיקה 4 יחידות קיץ 2016

 

שאלה 7

 

נתונה הפונקציה   f(x) = (2 - x) / (x - 1)²

א. מצא את תחום ההגדרה של הפונקציה.

ב. מצא את נקודת החיתוך של גרף הפונקציה עם הצירים.

ג. מצא את האסימפטוטות של גרף הפונקציה המאונכות לצירים.

ד. מצא את תחומי העלייה ואת תחומי הירידה של הפונקציה.

ה. סרטט סקיצה של גרף הפונקציה.

ו. לפניך שלושה גרפים I , II , III.

איזה מן הגרפים מתאר את הנגזרת f'(x) ? נמק.

פתרון שאלה 7


א. תחום ההגדרה של הפונקציה

נדרוש כי המכנה בפונקציה יהיה שונה מ- 0 משום שחלוקה באפס אינה מוגדרת. לכן תחום ההגדרה עבור x כל מספר פרט ל- 1.

ב. נקודות חיתוך של גרף הפונקציה עם הצירים


נקודת חיתוך עם ציר y כאשר x = 0: 

 f(x) = (2 - x) / (x - 1)²

 f(0) = (2 - 0) / (0 - 1)²

 f(0) = 2  

נקודת חיתוך עם ציר y היא: (0,2)

נקודת חיתוך עם ציר x כאשר y=0:

 f(x) = (2 - x) / (x - 1)²

 (2 - x) / (x - 1)² = 0

2 - x = 0

x=2

נקודת חיתוך עם ציר x היא: (2,0)

נסכם כי נקודות החיתוך עם הצירים הם: (0,2) , (2,0)

 

 

 ג. אסימפטוטות של   f(x) = (2 - x) / (x - 1)²

 

אסימפטוטה מאונכת לציר x

אסימפטוטה מאונכת לציר x בנקודה כלשהי נניח x = a תתקבל אם נשאיף את x ל- a, אזי הפונקציה f(x) תשאף לאינסוף. ניתן לראות שכאשר (x שואף ל- 1) x --> 1 הפונקציה f(x) שואפת לאינסוף. לכן יש אסימפטוטה מאונכת לציר x בנקודה x = 1, או המילים אחרות הישר x = 1 הוא אסימפטוטה.

 

אסימפטוטה מאונכת לציר y

אסימפטוטה מאונכת לציר y בנקודה כלשהי נניח y= b תתקבל אם נשאיף את x לאינסוף, אזי הפונקציה f(x) תשאף ל- b.

אם נשאיף את x לאינסוף אזי f(x) ישאף לאפס מאחר ובמונה המעלה של x היא 1 ובמכנה המעלה של x היא 2.

לכן הישר y = 0 הוא אסימפטוטה לפונקציה f(x) מאונכת לציר y.

 

גרף מהירות - פתרון שאלה 2 בגרות מתמטיקה 3 יחידות חורף תשפ"א 2021

  לצפייה / הורדת בגרות מתמטיקה 3 יחידות חורף  תשפ"א 2021, הקלק כאן

 

שאלה 2

הגרף שלפניך מתאר מהירות של רוכב אופניים בכל רגע בין השעה 8:00 לשעה 13:00 .

עיין בגרף וענה על הסעיפים א-ה שלפניך.

א. באיזו שעה הייתה מהירות הרוכב הגבוהה ביותר? מהי מהירות זו

ב . מאיזו שעה ועד איזו שעה היה הרוכב במנוחה?

ג . מה הייתה מהירות הרוכב בשעה 12:15 ?

ד. באילו פרקי זמן (בין איזו שעה לאיזו שעה) הייתה מהירות הרוכב במגמת עלייה?

ה. באילו שעות הייתה מהירות הרוכב 20 קמ"ש?

 

פתרון שאלה 2

א.מהירות הגבוהה של הרוכב

גרף המהירות מתאר את מהירות רוכב האופניים בזמן (בין השעות 8-13). השעה שבה מהירות הרוכב הייתה הגבוהה ביותר, היא הנקודה שבה הגרף הוא בערכו המקסימלי וזה כפי שניתן לראות בשעה 9:30. ערכה של מהירות זו ניתן לראות בגרף היא 30 קמ"ש.

ב . מאיזו שעה ועד איזו שעה היה הרוכב במנוחה?

תחום השעות בהן רוכב האופניים במנוחה

הרוכב במנוחה או למעשה מהירות היא 0 יתבטא אשר גרף המהירות מתלכד עם ציר x. כפי שניתן לראות בגרף מהירות רוכב האופניים היא אפס (הרוכב במנוחה) בין השעות 11:00 ל- 12:00.

ג. כפי שניתן לראות בגרף בשעה 12:15 מהירות הרוכב הייתה 10 קמ"ש.

ד. תחום השעות בהן מהירות הרוכב במגמת עליה

תחום השעות בהן מהירות הרוכב במגמת עליה

מהירות הרוכב במגמת עליה מתבטאת בגרף כעליה של גרף המהירות עם הזמן.

 וזה קורה בתחום בין השעה 8:00  ל- 9:30 ,  ובין השעה 12:00 ל- 13:00.

ה. השעות בהן הייתה מהירות הרוכב 20 קמ"ש

כדי לראות בגרף באילו שעות הייתה מהירות הרוכב 20 קמ"ש, נמתח קו ישר אופקי היוצא מציר המהירות (ציר y) בנקודה 20 קמ"ש ונבדוק באילו שעות הוא חותך את גרף המהירות. זה קורה בשעות: 9:00, 10:00, 12:30.

השעות בהן מהירות הרוכב הייתה 20 קמ"ש

 

פתרון שאלה 6 בגרות מתמטיקה 3 יחידות חורף תשפ"א 2021

 לצפיה / הורדת בגרות מתמטיקה 3 יחידות חורף  תשפ"א 2021, הקלק כאן

 

שאלה 6 - הסתברות וסטטיסטיקה

נתונים שני סביבונים, סביבון א' וסביבון ב'. על כל אחד מן הסביבונים כתובים ארבעה מספרים בדיוק:

 4 , 3 , 2 , 1 (על כל צד של סביבון כתוב מספר אחד בלבד).

ההסתברות שכאשר ייפול סביבון, יתקבל כל אחד מן המספרים האלה היא זהה.

מסובבים את שני הסביבונים ומחשבים את סכום המספרים שמתקבלים.

א. השלם בטבלה שלפניך את הסכומים שיכולים להתקבל.

ב. מהי ההסתברות שסכום המספרים שיתקבלו יהיה 4 ?

ג. מהי ההסתברות שסכום המספרים שיתקבלו יהיה גדול מ־ 5 ?

ד. מהי ההסתברות שסכום המספרים שיתקבלו יהיה מספר זוגי?

פתרון שאלה 6

 

א. השלמת טבלת הסכומים האפשריים המתקבלים משני הסביבונים

המספרים בטבלה הם סכומים אפשריים של המספרים המתקבלים מזריקת הסביבונים. לפיכך בכל משבצת יוצג סכום המספרים של סביבון א וסביבון ב.

ב. ההסתברות שסכום המספרים המתקבל הוא 4

ההסתברות שכאשר ייפול סביבון, יתקבל כל אחד מן המספרים היא זהה, ולכן גם ההסתברות שיתקבל הסכום של המספרים של שני הסביבונים זהה. כלומר ההסתברות לקבל כל מספר מבין 16 המספרים בטבלה לעיל זהה.

המספר 4 מופיע 3 פעמים ולכן ההסתברות לקבל סכום 4 היא 3/16.

ג. ההסתברות שסכום המספרים יהיה גדול מ- 5.

המספרים בטבלה הגדולים מ- 5 והופעותיהם הם: 6, 6, 7, 6, 7, 8. 

כלומר הופיע 6 פעמים סכום גדול מ- 5,  מתוך 16 . לכן ההסתברות להופעת סכום גדול מ- 5 הוא 6/16 = 3/8.

ד. ההסתברות שסכום המספרים שיתקבלו יהיה מספר זוגי.

נבדוק הסכומים הזוגיים המופעים בטבלה והופעותיהם: 2, 4, 4 ,6 , 4 , 6 , 6 , 8.

כלומר הופיע 8 פעמים סכום זוגי ,  מתוך 16 . לכן ההסתברות להופעת סכום זוגי הוא 8/16 = 1/2.

 

הסתברות וסטטיסטיקה - פתרון שאלה מספר 6 - ממבחן בגרות מתמטיקה 3 יחידות לימוד חורף 2022

מתוך מבחן בגרות מתמטיקה 3 יחידות לימוד חורף 2022 , מספר שאלון 035182.

שאלה 6 - הסתברות וסטטיסטיקה

יואב נבחן במשך שנת הלימודים בחמישה מבחנים רגילים במתמטיקה.

הציונים שקיבל יואב במבחנים אלה הם: 73 , 84 , 76 , 92 , 100 .

א. (1) מהו הציון הממוצע של יואב במבחנים הרגילים במתמטיקה?

(2) אם נבחר באקראי אחד מחמשת הציונים האלה, מהי ההסתברות שהציון שנבחר יהיה גבוה מן הציון הממוצע?

בסוף השנה נבחן יואב במבחן מסכם במתמטיקה וקיבל עליו את הציון 90 .

המורה קבעה שהציון השנתי הסופי במתמטיקה יחושב כך:

60% ממנו הוא הציון הממוצע של חמשת המבחנים הרגילים שהתלמיד נבחן בהם במשך השנה, ו־ 40% ממנו הוא הציון של המבחן המסכם.

ב. מהו הציון השנתי הסופי במתמטיקה שקיבל יואב?

פתרון שאלה 6

 א. (1) לחישוב ממוצע הציונים M, נסכם את חמשת הציונים ונחלק ב- 5.

M = (73 + 84 + 76 + 92 + 100) / 5 = 425 / 5 = 85

 הציון הממוצע של יואב במבחנים הרגילים במתמטיקה הוא 85.

 (2). הציונים שקיבל יואב במבחנים הם: 73 , 84 , 76 , 92 , 100 . והציון הממוצע הוא 85.  ניתן לראות כי  שני ציונים 92, 100 גבוהים מהציון הממוצע 85.

לכן אם נבחר באקראי אחד מחמשת הציונים האלה, ההסתברות שהציון שנבחר יהיה גבוה מן הציון הממוצע הוא 2/5 = 0.4.

 

ב. המורה קבעה שהציון השנתי הסופי במתמטיקה של יואב יחושב כך: 60% ממנו הוא הציון הממוצע של חמשת המבחנים הרגילים שהתלמיד נבחן בהם במשך השנה דהיינו 60% מ- 85, ו־ 40% ממנו הוא הציון של המבחן המסכם, דהיינו 40% מ- 90.

לכן הציון השנתי G של יואב הוא:

G = 60% * 85 + 40% * 90 = 51 + 36 = 87

 הציון השנתי של יואב הוא 87.

חוצה זוית במשולש ישר זוית - מבגרות מתמטיקה 3 יחידות חורף 2022

מתוך מבחן בגרות מתמטיקה 3 יחידות לימוד חורף 2022 , מספר שאלון 035182.

 

שאלה מספר 5

לפניך משולש ישר זווית ∡BCA = 90^o , ABC (ראה סרטוט).

 D היא נקודה על הצלע  CB .

AD חוצה את  CAB∡ .

נתון:  CAB = 58^o∡

12 ס"מ = . AD

א. מצא את אורך הצלע  AC .

ב. מצא את אורך הצלע  BC .

ג. מצא את היקף המשולש ABC.

 

פתרון שאלה 5

א. מציאת אורך הצלע AC.

נתבונן במשולש ACD.

1) AD חוצה את זוית CAB  - נתון

2)  CAB=58^o∡ - נתון

3) מכאן    CAD = 29^o∡ -נובע מ- 1) ו- 2).

4) זוית C ישרה - נתון, זוית משותפת למשולשים ABC, ADC.

5) מכאן שמשולש ADC:

AC = AD ᐧ cos( ∡CAB )  = 12 * cos(29^o) = 10.495

 

ב. מציאת את אורך הצלע  BC

 נתבונן במשולש ABC.

AC = 10.495 - חושב בסעיף א

  CAB=58^o∡   -  נתון

במשולש ABC:

tan(∡CAB) = BC / AC

נציב :

tan(58^o) = BC/10.495

1.600 = BC / 10.495

BC = 1.6 ᐧ 10.495 = 16.79

 

ג. מציאת היקף המשולש ABC.

משולש ABC הוא משולש ישר זווית (נתון זווית BAC ישרה). אורכי הניצבים AC, BC חושבו בסעיפים א,ב.

למציאת היקף המשולש ABC נחשב את אורך היתר AB באמצעות משפט פיתגורס, ונסכם את אורכי הניצבים והיתר לחישוב ההיקף.

על פי משפט פיתגורס , במשולש ישר זוית סכום ריבועי הניצבים שווה לריבוע היתר. כלומר במשולש ישר זווית ABC מתקיים:

AC² + BC² = AB²

נציב ונקבל:

10.495² + 16.76² = AB²

110.14 + 281.9 = AB²

392.04 = AB²

AB = 19.8

 ההיקף P של משולש ABC הוא סכום צלעותיו, הניצבים AC, BC והיתר AB, כלומר:

P = AB + BC + AC = 19.8 + 16.79 + 10.495 = 47.085