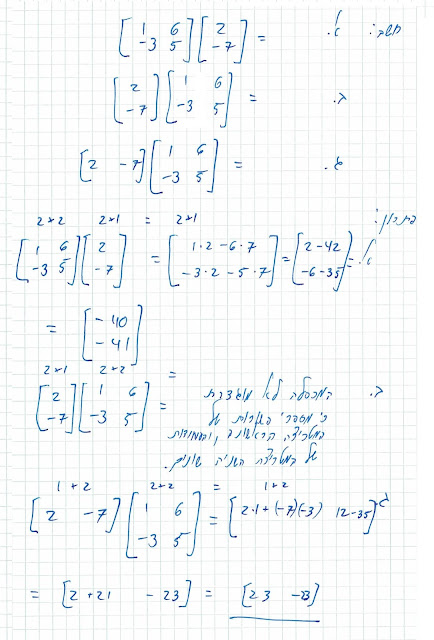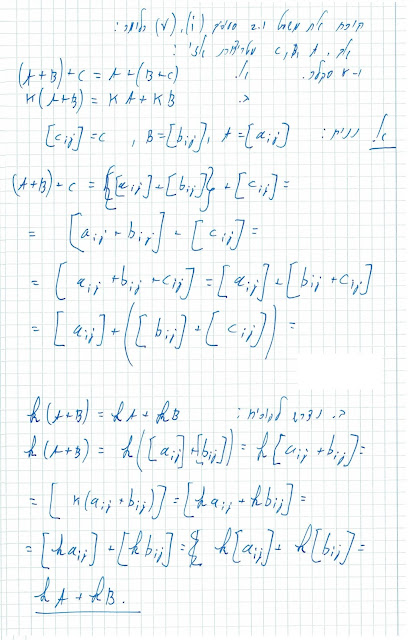אלגברה לינארית - אורתוגונליות ומשוואת מישור

אלגברה לינארית - אורתוגונליות ומשוואת מישור

אלגברה לינארית - שלילת חוק החילוף בכפל מטריצות

שלילת חוק החילוף בכפל מטריצות

המכפלה B*A אינה מוגדרת מאחר ומספר העמודות של מטריצה B , (3 עמודות) ,שונה ממספר השורות של מטריצה  A (3 שורות).

אלגברה לינארית - כפל מטריצות - דוגמא פתורה

אלגברה לינארית - כפל מטריצות - דוגמא פתורה

אלגברה לינארית - כפל מטריצות

כפל מטריצות דוגמאות פתורות

בגרות מתמטיקה 4 יחידות קיץ 2019 שאלון ראשון - גיאומטריה אנליטית

מתוך בגרות מתמטיקה 4 יחידות קיץ 2019 שאלון ראשון - שאלה 2

שאלה 2

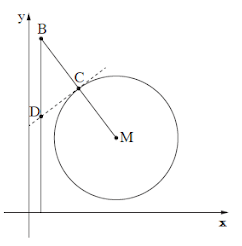
נתון מעגל שמרכזו M(7, 6) . הישר MB חותך את המעגל בנקודה C (ראה איור).

 

מעגל שמרכזו M(7, 6) . הישר MB חותך את המעגל בנקודה C

נתון B(1, 14) ,

MC = BC.

א. מצא את משוואת המעגל.

העבירו משיק בנקודה C.

ב. מצא את משוואת המשיק.

מן הנקודה B הורידו אנך לציר x . המשיק טהאנך נחתכים בנקודה D.

ג. חשב את שטח המשולש BCD.

הנקודה E נמצאת על האנך שהורידו מנקודה B לציר x.

נתון: ME||CD.

ד. מצא את שיעורי הנקודה E.

ה. הראה כי נקודה D היא מרכז המעגל החוסם את משולש BME.

פתרון שאלה 2

א. מציאת משוואת המעגל.
למציאת משוואת המעגל נחוצים הקואורדינטות של מרכזו הנתונות בנקודה M (7,6), ורדיוס המעגל שהוא שווה ל- MC השווה למחצית MB.

נחשב את אורך הקטע MB:
 שיעור הנקודה M הוא (7,6)
שיעור הנקודה B(1,14)

לכן אורך הקטע MB:


לפנינו מעגל שמרכזו בנקודה 7,6 ורדיוסו 5, לכן משוואת המעגל:




ב. משוואת המשיק למעגל בנקודה C

למציאת משוואת המשיק בנקודה C נמצא את שיעורי הנקודה C ואת שיפוע המשיק ועל פיהם נחשב את משוואת המשיק. הנקודה C היא מרכז הקטע MB, ושיפוע המשיק מאונך לשיפוע MB הואיל ומשיק מאונך לרדיוס (MC על קטע MB) בנקודת ההשקה.

ג. שטח המשולש BCD

בגרות מתמטיקה 4 יחידות קיץ 2019 שאלון ראשון - בעיית מהירות

מתוך בגרות מתמטיקה 4 יחידות קיץ 2019 שאלון ראשון - שאלה 1

שאלה 1

המרחק בין עיר א' לעיר ב' הוא 120 ק"מ.
מכונית נסעה בבוקר מעיר א' לעיר ב' במהירות קבועה.
בערב חזרה המכונית מעיר ב' לעיר א' באותה הדרך. המכונית נסעה במשך שעה באותה המהירות שבה נסעה בבוקר. היא עצרה בצד הדרך למשך 2 דקות, ולאחר מכן המשיכה בנסיעתה עד עיר א' במהירות הגבוהה ב־ 10 קמ"ש ממהירות נסיעתה בבוקר.
זמן הנסיעה של המכונית בערב (כולל משך זמן העצירה) היה שווה לזמן הנסיעה שלה בבוקר.

א. מצא את מהירות המכונית בבוקר.
ב. השעה שבה יצאה המכונית מעיר ב' בדרכה חזרה לעיר א' הייתה שמונה בערב.
מה היה המרחק שלה מעיר א' בשעה תשע ו־ 8 דקות בערב?

פתרון שאלה 1

ניתן לתאר את מסלולי נסיעת המכונית מעיר א לעיר ב וחזרה באמצעות טבלה.
נסמן:
v - מהירות נסיעת המכונית מעיר א לעיר ב.
t – זמן נסיעת המכונית מעיר א לעיר ב.

טבלת תיאור מסלולי נסיעת המכונית מעיר א לעיר ב וחזרה

 פתרון סעיף א

משוואות שוויון מרחק מעיר א לעיר ב:

v*t = 120
(v + 10) * [ t - (1 + 2/60)] + v*1 = 12

(v + 10) * (t - 62/60) + v = 12

vt - 62v/60 +10t -62/6 = 120 = vt

10t - 62/6 = 2v/60

600t -620 = 2v

v = 300t - 310

 נציב ב- v*t = 120 ונקבל:

(300t - 310) * t = 120

300t² - 310t -120 =0

30t² - 31t -12 =0

קיבלנו משוואה ריבועית. פותרים עבור t ומקבלים:

t1 = 4/3

t2 = -0.3

מאחר ו- t חיובי הפתרון הוא t= 4/3

v = 120/t = 120 / (4/3) = 90

מהירות המכונית בבוקר היא 90 קמ״ש.

פתרון סעיף ב

על פי נתוני השאלה בסעיף ב, השעה שבה יצאה המכונית מעיר ב' בדרכה חזרה לעיר א' הייתה שמונה בערב.

 בשעה 9 ושמונה דקות בערב הייתה המכונית לאחר שעה נסיעה במהירות 90 קמ"ש, ועוד 6 דקות נסיעה (לאחר 2 דקות עצירה) במהירות 100 קמ"ש.

לכן המרחק של המכונית מעיר ב':

90 ᐧ 1 + 100 ᐧ 6 / 60 = 90 + 10 = 100

המרחק של המכונית מעיר ב' בשעה 9 ושמונה דקות היה 100 ק"מ.

 המרחק של המכונית מעיר א':

20 = 100 - 120

 המרחק של המכונית מעיר א' בשעה 9 ושמונה דקות הוא 20 ק"מ.

 

בגרות 3 יחידות לימוד מתמטיקה חורף 2020 - בעיית מהירות עם גרף

מתוך שאלון בגרות 3 יחידות מתמטיקה חורף 2020 - שאלון ראשון שאלה 2

שאלה 2

רוכב אופניים יצא מביתו והחל לרכוב. הגרף שלפניך מתאר את המרחק של הרוכב מביתו כפונקציה של הזמן.

עיין בגרף וענה על הסעיפים א-ה.

א. באיזה מרחק מביתו היה רוכב האופניים בשעה 11:30?

ב. באילו שעות היה רוכב האופניים במרחק 10 ק"מ מביתו?

ג. כמה פעמים עצר רוכב האופניים, וכמה זמן נמשכה כל עצירה?

ד. כמה קילומטרים עבר רוכב האופניים מן השעה 13:00 עד השעה 14:00?

ה. מאיזו שעה עד איזו שעה נסע רוכב האופניים במהירות הגדולה ביותר?

פתרון שאלה 2

סעיף א

בשעה 11:30 היה הרוכב במרחק 30 ק"מ מביתו. (ראה גרף 1 )

גרף 1- בשעה 11:30 היה הרוכב במרחק 30 ק"מ מביתו.

סעיף ב

הרוכב היה במרחק 10 ק"מ מביתו בשעות  7:30 , 13:45 . (ראה גרף 2)

גרף 2 - הרוכב היה במרחק 10 ק"מ מביתו בשעות  7:30 , 13:45

סעיף ג- עצירות רוכב האופניים

רוכב האופניים עצר שתי עצירות. העצירה הראשונה בין השעות 9:00-11:00 למשך שעתיים, והעצירה השניה בין השעות 12-13 למשך שעה. סה"כ עצר רוכב האופניים למשך 3 שעות.

גרף 3 - עצירות רוכב האופניים

סעיף ד - המרחק שעבר רוכב האופניים מן השעה 13:00 עד השעה 14:00

ניתן לראות כי בשעה 13:00 היה רוכב האופניים במרחק 40 ק"מ מהבית, ובשעה 14:00 היה רוכב האופניים בבית, לכן בין השעות 13:00- 14:00 עבר רוכב האופניים 40 ק"מ

המרחק שעבר רוכב האופניים מן השעה 13:00 עד השעה 14:00

 סעיף ה- הזמן שבו נסע רוכב האופניים במהירות הגבוהה ביותר

רוכב האופניים נסע במהירות הגבוהה ביותר בתחום השעות 13:00-14:00 , ניתן לראות זאת על פי שיפוע הגרף התלול ביותר וגם על פי כך שבמשך שעה אחת בין השעות 13:00 - 14:00  עבר רוכב האופניים את המרחק הגבוה ביותר למשך שעה (מהירות 40 קמ"ש)

מכפלת מטריצות - מספר שורות ועמודות

מכפלת מטריצות - מספר שורות ועמודות של המטריצה המתקבלת ותחום הגדרה

מכפלת מטריצות

מכפלת מטריצות - דוגמא פתורה

חשב:

 

פתרון

 

ג. המכפלה אינה מוגדרת מאחר ומספר העמודות במטריצה השמאלית (4) שונה ממספר השורות במטריצה הימנית (3).

חיבור מטריצות וכפל בסקלר - הוכחת משפטים

חיבור מטריצות וכפל בסקלר עם נעלמים

 חיבור מטריצות וכפל בסקלר עם נעלמים - תרגיל פתור

חיבור מטריצות וכפל בסקלר

חיבור מטריצות וכפל בסקלר - תרגיל פתור

בגרות 3 יחידות לימוד מתמטיקה - פתרון בעיה כללית

מתוך שאלון בגרות 3 יחידות מתמטיקה חורף 2020 - שאלון ראשון שאלה 1

שאלה 1

המחיר של חולצה נמוך ב- 60 שקלים מן המחיר של שמלה.
א. סמן ב- x את המחיר של שמלה, והבע באמצעות x את מחיר החולצה.
ב. אלונה קנתה 4 חולצות ו- 3 שמלות ושילמה עבורם 810 שקלים. מהו המחיר של שמלה?

פתרון שאלה 1

א.
נסמן ב- x את מחיר השמלה. מחיר החולצה נמוך ב- 60 שקלים ממחיר השמלה, ולכ מחיר החולצה יסומן x-60.

מחיר שמלה: x
מחיר חולצה: x-60

ב.
אלונה קנתה 4 חולצות ו- 3 שמלות ושילמה עבורם 810 שקלים, לכן:

נפתור:


מחיר שמלה 150 שקל, ומחיר חולצה 90 שקל.

מציאת אורך (נורמה) של וקטור

אלגברה לינארית - תרגיל פתור וקטורים

ו. מציאת המרחק בין הוקטורים u, v (sqrt - שורש ריבועי) :

d(u, v) = ||u - v|| = ||(1, -2, 4) - (3, 5, 1)|| = ||(-2, -7, 3)|| =

sqrt[(-2)² + (-7)² + 3²] = sqrt(4 + 49 + 9)  = √(62)

ז. מציאת proj(u, v)

 proj(u, v) = uᐧv / ||v||² ᐧ v = -3 / 35 ᐧ (3, 5, 1) = ( -9/35 , -3/7 , -3 / 35)

אלגברה לינארית - זוית בין וקטורים, מרחק בין וקטורים ו- proj(u,v)

אלגברה לינארית -נירמול וקטורים

אלגברה לינארית - הוכחת תכונות של מכפלה סקלרית של וקטורים

הוכחת תכונות של מכפלה סקלרית של וקטורים

חוק הפילוג (דיסטריביוטיביות)

חוק הקיבוץ (אסוציאטיביות)

חוק החילוף (קומוטטיביות)

הוכחת אי שוויון מיניקובסקי

הוכח את אי שוויון מינקובסקי:

|| u + v || ≤ || u || + || v ||

הוכחה:

|| u + v ||² = (u +v)(u +v) = u² + 2uv + v² = || u ||² + 2uv + || v ||² =

מאי שוויון קושי שוורץ:

 || u ||² + 2uv + || v ||²  ≤  || u ||² + 2·|| u || · || v || + || v ||² = (|| u || + || v ||)² 

לכן:

|| u + v || ≤ || u || + || v ||

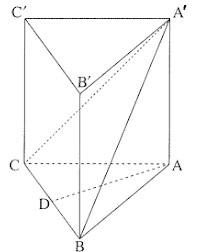
טריגונומטריה במרחב - מנסרה ישרה משולשת - מבגרות 4 יחידות לימוד מתמטיקה

מתוך שאלון בגרות 4 יחידות מתמטיקה קיץ 2019 - שאלון שני - שאלה 2

 

טריגונומטריה במרחב

2. ' ABCA'B'C היא מנסרה משולשת וישרה שבסיסה הוא משולש שווה שוקיים (AB = AC) .
הנקודה D היא אמצע הקטע BC (ראה ציור).

 

נתון: AD = 12 , זווית CAB שווה 40 מעלות.

א. חשב את אורך הצלע BC.
ב. הסבר מדוע המשולש CA'B הוא משולש שווה שוקיים.

נתון כי שטח המשולש CA'B הוא 80.
ג. חשב את גודל הזווית שבין הקטע ' DA ובין בסיס המנסרה ABC.
ד. חשב את נפח המנסרה ' ABCA'B'C.

 

 

פתרון

סעיף א - חישוב אורך הצלע BC 

 

אלגברה לינארית - חיבור וחיסור וקטורים

אלגברה לינארית - פעולות אריתמטיות בסיסיות בוקטורים

מצא את x ואת y כאשר:

א. 

(x, 3) = (2, x + y)

פתרון

(x, 3) = (2, x + y)

x = 2

3 = x + y

3 = 2 + y

y = 1

x = 2

ב. 

(4, y) = xᐧ(2 , 3)

פתרון

(4, y) = xᐧ(2 , 3)

(4, y) = (2x , 3x)

4 = 2x

y = 3x

x = 2

y = 3*2 = 6

x = 2

y = 6

אלגברה לינארית - דוגמא פתורה: קומבינציה לינארית של וקטורים

אלגברה לינארית - דוגמא פתורה: קומבינציה לינארית של וקטורים

אלגברה לינארית - דוגמא פתורה: קומבינציה לינארית של וקטורים

אלגברה לינארית - מכפלה פנימית של וקטורים

מכפלה פנימית של וקטורים:

מצא את u∙v כאשר:

א.

u = (2 , -5, 6)

v = (8, 2 ,-3)

ב.

u = ( 4 , 2, -3 , 5, -1)

v = (2 , 6, -1 , -4 , 8)

מכפלה פנימית של וקטורים 

u = (u₁, u₂, u₃, …. u_n)

v = (v₁, v₂, v₃, …. v_n)

המכפלה הפנימית של וקטורים u, v מוגדרת

u∙v =  (u₁∙v₁ + u₂∙v₂ + …. + u_n∙v_n)

 

נפתור:

א.

u = (2 , -5, 6)

v = (8, 2 ,-3)

u∙v = 2*8 - 5*2 - 6*3 = 16 -10 -18 = -12

ב. 

u = ( 4 , 2, -3 , 5, -1)

v = (2 , 6, -1 , -4 , 8)

u∙v = 4*2 + 2*6 +3*1 - 5*4 -1*8 = 8 +12 +3 -20 - 8 = -5

משפט Cauchy Schwartz - קושי שוורץ

משפט Cauchy Schwartz

 

וקטורים אורתוגונלים - דוגמא פתורה

שאלה

נתונים הוקטורים:

u = (5, 4, 1)

v = (3, -4, 1)

w = (1, -2, 3)

אילו צמדים של וקטורים (אם בכלל) הם אורתוגונלים?

פתרון

תנאי אורתוגונליות של שני וקטורים u, v הוא שמכפלתם הסקלרית שווה 0. כלומר u * v = 0 .

נבדוק אורתוגונליות עבור כל צמד וקטורים.

u * v = (5, 4, 1) * (3, -4, 1) = 5 * 3 + 4 * (-4) + 1 * 1  = 15 - 16 + 1 = 0

u, v אורתוגונלים.

u * w = (5, 4, 1) * (1, -2, 3) = 5 -8 + 3 = 0

u, w אורתוגונלים.

v * w = (3, -4, 1)  * (1, -2, 3) =  3 + 8 + 3 = 14

v, w לא אורתוגונלים.

וקטורים אורתוגונלים - אלגברה לינארית

שאלה

מצא עבור אלו ערכים של k הוקטורים u, v אורתוגונליים?

א. 

u = (1, k, -3)

v = (2, -5, 4)

פתרון סעיף א

נפעיל את תנאי האורתוגונליות של וקטורים : u * v = 0, ונמצא את k המתאים:

u * v = (1, k, -3) * (2, -5, 4) = 1 * 2 + k * (-5) + (-3) * 4 = 2 - 5k -12 = -10 - 5k = 0

-10 - 5k = 0

5k = -10

k = -2

הוקטורים u, v אורתוגונליים עבור k = -2.

ב.

u = (2, 3k, -4, 1 , 5)

v = (6, -1, 3, 7, 2k)

פתרון סעיף ב

נפעיל את תנאי האורתוגונליות של וקטורים : u * v = 0, ונמצא את k המתאים:

u * v = (2, 3k, -4, 1 , 5) * (6, -1, 3, 7, 2k) = 2 * 6 + 3k * (-1) + (-4) * 3 + 1 * 7 + 5 * 2k = 0

12 - 3k - 12 + 7 + 10k = 0

7k + 7 = 0

7k = -7

k = -1

הוקטורים u, v אורתוגונליים עבור k = -1..

חקירת פונקציה לוגריתמית - מבגרות 4 יחידות לימוד מתמטיקה קיץ 2019

מתוך שאלון בגרות 4 יחידות מתמטיקה קיץ 2019 - שאלון שני - שאלה 5

שאלה 

נתונה הפונקציה     f(x) = ln(-x² + ax)  ,  שתחום ההגדרה שלה הוא  a>x>0 .

 a > 0 הוא פרמטר.

ידוע כי לפונקציה f(x) יש נקודת קיצון.

א. הראה כי שיעור ה - x  של נקודת הקיצון של הפונקציה f(x) הוא a/2 .

נתון כי שיעור ה- y של נקודת הקיצון של הפונקציה f(x)  הוא   ln(2.25)  .

ב. מצא את a.

הצב a = 3 במשוואת הפונקציה f(x) ובתחום ההגדרה שלה, וענה על סעיפים ג-ד.

ג. קבע את סוג נקודת הקיצון של הפונקציה f(x).

ד. (1) מצא את שיעורי נקודות החיתוך של גרף הפונקציה f(x) עם ציר ה-x.

    בתשובתך השאר 2 ספרות אחרי הנקודה העשרונית.

    (2) מצא את משוואות האסימפטוטות של הפונקציה f(x) המאונכות לציר x.

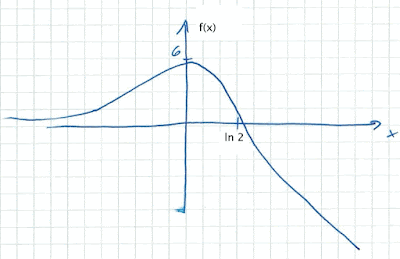
    (3) סרטט סקיצה של גרף הפונקציה f(x).

פתרון 

א. שיעור נקודת הקיצון

נתונה הפונקציה     f(x) = ln(-x² + ax)  ,  שתחום ההגדרה שלה הוא  a>x>0 .

 a > 0 הוא פרמטר.

נדרש להוכיח כי f(a/2) היא נקודת קיצון. 

נמצא נקודת קיצון של  f(x)  על ידי פתרון המשוואה: f'(x) = 0 .

f'(x) = (-2x + a) / (-x² + ax) = 0

f'(x) = (-2x + a) / [x(-x + a)] = 0

המכנה חיובי וגדול מאפס מאחר ו-  a>x>0 ,  a>0 .

ולכן:

-2x + a = 0

x = a /2

נחשב את f(a / 2) :

f(a / 2) =  ln[-(a/2)² + a(a/2)] = ln(-a²/4 + a²/2) = ln(a²/4) 

f(a / 2) = ln(a²/4) 

שיעור נקודת הקיצון הוא:    ( a / 2 ,  ln(a²/4) ).

ב. מציאת הפרמטר a

נתון ערך מספרי לשיעור נקודת הקיצון:   f(a/2) = ln(2.25)

מכאן:  a² / 4 = 2.25

a² / 4 = 2.25

a²  = 9

a = ±3

הפתרון a = -3 נפסל בגלל התנאי  a  > 0 .

לכן הפתרון הוא a = 3

ג. סוג נקודת הקיצון:

בסעיף א מצאנו כי שיעור נקודת הקיצון הוא:    ( a / 2 ,  ln(a²/4) ). נציב  a = 3 ונקבל שיעור נקודת קיצון:

( a / 2 ,  ln(a²/4)  = (3 / 2 , ln(3² / 4) = (1.5,  ln(2.25))

נבדוק ערכי f(x) עבור ערכי x השווים 1.6 , 1.4 .

f(1.4) = ln(-1.4² + 3*1.4) = ln(2.24)

f(1.6) = ln(-1.6² + 3*1.6) = ln(2.24)

ניתן לראות כי הנקודה x = 1.5 היא נקודת מקסימום משום שערכי f(x) בנקודות לידה קטנות יותר.

לכן סוג נקודת הקיצון של f(x) הוא מקסימום.

ד. (1) . נקודות חיתוך של f(x) עם ציר x.

למציאת נקודות חיתוך של f(x) עם ציר x נציב f(x) = 0:

  f(x) = ln(-x² + 3x)  = 0

-x² + 3x = e^0 = 1

x² - 3x + 1 = 0

נקודות חיתוך הפונקציה עם ציר x:

x1 = 2.61

x2 = 0.38

ד. (2). משוואת אסימפטוטות של הפונקציה המאונכות לציר x

נרשום את הפונקציה:   f(x) = ln(-x² + 3x) .

הפונקציה f(x) שואפת למינוס אינסוף כאשר הביטוי בתוך הלוג שואף ל- 0. כלומר כאשר:

-x² + 3x = 0

x(x - 3) = 0

x1 = 0

x2 = 3

משוואת אסימפטוטות של הפונקציה המאונכות לציר x  הן: x = 0 , x = 3.

ד. (3) . סקיצה של גרף הפונקציה :

תחום ההגדרה של הפונקציה הוא.  בין 0 ל- 3. 

לפונקציה נקודות חיתוך עם ציר x בנקודות : 2.61 , 0.38.

משוואת אסימפטוטות של הפונקציה המאונכות לציר x  הן: x = 0 , x = 3.

לפונקציה נקודת מקסימום: 

(1.5,  ln(2.25))  = (1.5,  0.81)

להלן סקיצה של גרף הפונקציה  f(x) = ln(-x² + 3x) :

סקיצה של גרף הפונקציה  f(x) = ln(-x² + 3x) 

חקירת פונקציה אקספוננציאלית - מבגרות 4 יחידות לימוד מתמטיקה 2019

מתוך שאלון בגרות 4 יחידות מתמטיקה קיץ 2019 - שאלון שני - שאלה 4

שאלה 4

נתונה הפונקציה f(x) = -3ᐧe^xᐧ(2ᐧe^x - 4) .

א. מצא את תחום ההגדרה של f(x).

ב. מצא את שיעורי החיתוך של גרף הפונקציה f(x) עם הצירים.

ג. מצא את שיעורי נקודות הקיצון של הפונקציה f(x), וקבע את סוגה.

ד. סרטט סקיצה של גרף הפונקציה f(x).

ה. נתונה הפונקציה g(x) = -(1/2)ᐧf(x).

(1) כתוב מה הם שיעורי נקודת הקיצון של הפונקציה g(x) , וקבע את סוגה.

(2) סרטט סקיצה של גרף הפונקציה g(x).

פתרון שאלה 4

א. תחום ההגדרה של הפונקציה   f(x) = -3ᐧe^xᐧ(2ᐧe^x - 4).  

ניתן לראות כי אין הגבלה לערך ש- x  יכול לקבל מאחר ואינו בשורש, מכנה .

ב. נקודות חיתוך הפונקציה f(x)  עם הצירים

נקודות חיתוך עם ציר y כאשר x =0. 

f(0) = -3ᐧe⁰ᐧ(2ᐧe⁰ - 4) = -3ᐧ(2 - 4) = 6

נקודת חיתוך עם ציר y היא: (6 , 0).

נקודות חיתוך עם ציר y כאשר f(x) =0. 

f(x) = -3ᐧe^xᐧ(2ᐧe^x - 4) = 0

e^xᐧ(2ᐧe^x - 4) =0

קיימות שתי אפשרויות לפתרון המשוואה.

אפשרות ראשונה:

e^x = 0

אין x המקיים משוואה זו.

אפשרות שניה:

2ᐧe^x - 4 = 0

2ᐧe^x = 4

e^x = 2

x = ln2

נקודת חיתוך עם ציר x היא: (0 , ln2).

נקודות החיתוך של הפונקציה f(x) עם הצירים:  (6 , 0) , (0 , ln2) .

ג. נקודות קיצון של הפונקציה f(x) וסוגיהן

ד. סקיצה של גרף הפונקציה f(x)

נרכז את הנתונים הידועים לנו על הפונקציה f(x).

f(x) = -3ᐧe^x(2ᐧe^x - 4)

נקודות חיתוך עם הצירים: (6 , 0) , (0 , ln2)

נקודת מקסימום: (6 , 0) .

סקיצה:

סקיצה של גרף הפונקציה f(x)

ניתן לראות שככל ש- x שואף ל- ∞- אז f(x) שואף ל- 0 . 

לכן קיימת אסימפטוטה לפונקציה אופקית y = 0.

ככל ש- x שואף ל- ∞+ אז f(x) שואף ל- ∞- , לפיכך הסקיצה שורטטה בהתאם. 

סעיף ה - פונקציה g(x): מציאת נקודות קיצון ושרטוט סקיצה

חקירת פונקציה טריגונומטרית - מבגרות 4 יחידות לימוד מתמטיקה

מתוך שאלון בגרות 4 יחידות מתמטיקה קיץ 2019 - שאלון שני - שאלה 3

שאלה 3

הפונקציה f(x) מוגדרת בתחום   k0 ≤ x ≤ π.

נתון   f'(x) = -3ᐧsin2x ,  f(0) = 0.75

פונקציית הנגזרת, f'(x) , מוגדרת גם היא בתחום   k0 ≤ x ≤ π.

א. מצא ביטוי אלגברי לפונקציה f(x) .

ב. מצא את שיעורי נקודות החיתוך של גרף הפונקציה f(x) עם ציר x.

ג. מצא את שיעורי כל נקודות הקיצון של הפונקציה f(x) בתחום הנתון, וקבע את סוגן.

ד. סרטט סקיצה של גרף הפונקציה f(x).

ה. חשב את השטח המוגבל על ידי גרף הפונקציה f(x) ועל ידי ציר ה- x בתחום שבין נקודות החיתוך שמצאת בסעיף ב.

פתרון שאלה 3

סעיף א - מציאת ביטוי אלגברי ל- f(x)

למציאת ביטוי אלגברי לפונקציה f(x) נבצע אינטגרציה לנגזרת שלה f'(x) = -3sin(2x) :

∫ f'(x)d = ∫ -3sin(2x)dx = (3/2)cos(2x) + c

f(x) = (3/2)cos(2x) + c

נתון f(0) = 0.75 והפונקציה מוגדרת בתחום :  k0 ≤ x ≤ π.

נציב x = 0 בפונקציה f(x) :

f(0) = (3/2)cos(2ᐧ0) + c = 0.75

3/2 + c = 0.75

c = -0.75

לכן:

f(x) = (3/2)ᐧcos(2x) - 0.75

סעיף ב - נקודות חיתוך הגרף עם הצירים

סעיף ג - מציאת שיעורי נקודות הקיצון וסוגן

סעיף ד - סקיצה של גרף הפונקציה f(x)

סעיף ה - השטח המוגבל בין גרף הפונקציה f(x) לנקודות החיתוך עם ציר ה- x