מתי מתוק: ספטמבר 2011

נוסחה כפל מספרים מרוכבים הצגה קוטבית + דוגמה פתורה

כפל מספרים מרוכבים - הצגה קוטבית

במילים אחרות:

בכפל של שני מספרים מרוכבים הערך המוחלט של המכפלה שווה למכפלת הערכים המוחלטים של שני המספרים, והארגומנט של המכפלה שווה לסכום הארגומנטים של שני המספרים.

משפט תאלס ההפוך: שני ישרים המקצים על שוקי זוית קטעים פרופורציונים – מקבילים זה לזה.

משפט תאלס ההפוך קובע שאם AB/AD = AC/AE

ישרים חותכים שוקי זווית

או אחד מיחסי הפרופורציה:
AB/BD = AC/CE או
AD/BD = AE/CE

אזי מתקיימת המקבילות:

DE||BC

קישורים:

משפט תאלס - שני ישרים מקבילים החותכים שוקי זווית מקצים עליהן קטעים פרופורציונים

יחסי פרופורציה - חוקים והוכחה

יחסי פרופורציה:

קישורים:

משפט תאלס - שני ישרים מקבילים החותכים שוקי זווית מקצים עליהן קטעים פרופורציונים

משפט תאלס - שני ישרים מקבילים החותכים שוקי זווית מקצים עליהן קטעים פרופורציונים

משפט תאלס קובע שאם DE||BC

שני ישרים מקבילים חותכים שוקי זוית

אזי מתקיים יחס הפרופורציה: AB/AD = AC/AE

כמו כן מתקיימות ע"פ חוקי יחסי פרופורציה ניתן להוכיח:
AB/BD = AC/CE
AD/BD = AE/CE

קישורים:

משפט תאלס ההפוך: שני ישרים המקצים על שוקי זוית קטעים פרופורציונים – מקבילים זה לזה.

אנכים לשוקיים במשולש שווה שוקיים - בעיה פתורה בגיאומטריה

שאלה

BD ו- CE הם גבהים לשוקיים במשולש שווה שוקיים ABC (הצלעות AB = AC).

א. הוכח כי המשולשים CEB, BDC חופפים.

ב. הוכח DE||BC.

ג. הוכח: AE*AC = AD*AB.

פתרון

נתון משולש שווה שוקיים AB = AC
BD ו- CE הם גבהים לשוקיים במשולש, BD מאונך ל- AC, ו- CE מאונך ל- AB

א. נוכיח שמשולשים BDC ו- CEB חופפים:
שני המשולשים הם ישרי זווית לפיכך נדרשים עוד שני שיוויונים במשולשים להוכיח חפיפתם.
זהות ראשונה: זווית CBE = זווית BCD - זוויות בסיס במשולש שווה שוקיים ABC שוות
זהות שניה: BC = BC - צלע משותפת
מכאן: משולשים BDC ו- CEB חופפים
מ.ש.ל א'

ב. נוכיח ש- DE||BC באמצעות משפט תאלס הפוך:
שני ישרים (BC, DE) המקצים על שוקי זווית (BAC) קטעים פרופורציונים (AE/BE = AD/DC) , מקבילים זה לזה.

(1) AB = AC - נתון
(2) BE = CD - נובע מהחפיפה שהוכחה ב- א
לכן:
(3) AE = AD , נובע מ- (1) ו- (2): חיסור גדלים שווים מגדלים שווים נותן גדלים שווים
AE/BE = AD/DC נובע מ- (2) ו- (3) חלוקת גדלים שווים מגדלים שווים נותן מנות שוות
לכן
DE||BC - משפט תאלס הפוך:
שני ישרים (BC, DE) המקצים על שוקי זווית (BAC) קטעים פרופורציונים (AE/BE = AD/DC) , מקבילים זה לזה.
מ.ש.ל ב

ג. נוכיח ש: AE*AC = AD*AB
נוכיח דימיון משולשים ABC, AED
זווית ABC = זווית AED - מתאימות מקבילים DE || BC (הוכח בסעיף ב) , חותך AB
זווית ACB = זווית ADE - מתאימות מקבילים DE || BC (הוכח בסעיף ב) , חותך AC
זווית A = זווית A - משותפת
מכאן משולשים ABC, AED דומים - משולשים ששלוש זוויותיהם (או שניים מהזוויות) שוות, דומים
מהדימיון נובע: AE/AB = AD/AC - יחסי צלעות מתאימות במשולשים דומים
מכאן AE*AC = AD*AB
מ.ש.ל

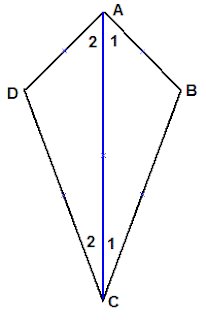משפט בגיאומטריה: האלכסון הראשי בדלתון חוצה את זוויות הראש

נתון דלתון ABCD ואלכסון ראשי AC

נדרש להוכיח כי האלכסון הראשי AC חוצה את זוויות הראש, כלומר:
זווית A1 = זווית A2
זווית C1 = זווית C2

הוכחה
חופפים את משולשים ABC, ADC לפי צ.צ.צ:
AB = AD נתון מהגדרת הדלתון - צלעות סמוכות לזווית הראש שוות
CB = CD נתון מהגדרת הדלתון - צלעות סמוכות לזווית הראש שוות
AC = AC צלע משותפת
מכאן:
משולש ABC שווה וחופף למשולש ADC
מהחפיפה נובע:
זווית A1 = זווית A2
זווית C1 = זווית C2
מ.ש.ל

בעיה פתורה במכניקה קינטיקה - תנועה שוות תאוצה - מזחלת שלג גולשת במורד גבעה

קישורים:

משפט : זוויות נגדיות במקבילית שוות זו לזו

נתונה מקבילית ABCD

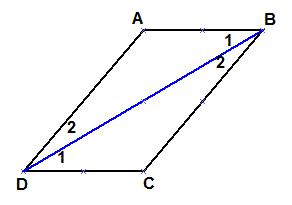מקבילית ABCD ואלכסון BD

נדרש להוכיח

זווית ABC = זווית ADC (זווית B שווה לזווית D)

הוכחה

תחילה בונים בניית עזר את האלכסון BD,
זווית B1 = זווית D1 - פנימיות מתחלפות AB||CD חותך BD
זווית B2 = זווית D2 - פנימיות מתחלפות AD||BC חותך BD

מכאן : זווית B1 + זווית B2 = זווית D1 + זווית D2
מכאן: זווית B = זווית D
מ.ש.ל

באותה דרך ניתן לבנות האלכסון AC כבניתת עזר ולהוכיח שיוויון זוויות A ו- C.

משפט בגיאומטריה: אלכסונים במלבן שווים זה לזה

נתון מלבן ABCD
נדרש להוכיח כי האלכסון AC שווה לאלכסון BD.

ניתן להוכיח ע"י חפיפת משולש BCD למשולש ADC
AD = BC - צלעות נגדיות במלבן שוות
CD = CD - צלע משותפת
זווית ADC = זווית BCD - כל זוויות המלבן ישרות ולכן שוות

מכאן: משולש BCD שווה וחופף למשולש ADC צ.ז.צ

מהחפיפה נובע: AC = BD
מ.ש.ל

סכום הזויות במשולש שווה 180°

שיטת ההוכחה - בונים מקביל a לבסיס המשולש AB העובר דרך קודקוד C. מוכיחים כי הזוויות הנוצרות בין המקביל לצלעות המשולש שוות לזוויות המשולש ע"פ שיוויון זוויות בין מקבילים וחותך, סכום הזוויות על המקביל a שווה 180 מעלות ולכן סכום זוויות המשולש שווה 180 מעלות

נתון : משולש ABC

נדרש להוכיח: סכום הזוויות במשולש שווה 180°.

הוכחה

בניית עזר: בונים את הישר a העובר דרך קודקוד C ומקביל לצלע AB.

מסמנים את זוויות המשולש ABC באותיות: 𝜶 , β , ɣ , ואת הזוויות הנוצרות עם הישר המקביל a באותיות '𝜶' , β כמשורטט בשרטוט לעיל.

1. 𝜶' = 𝜶 - זוויות פנימיות מתחלפות a || AB , חותך AC.

2. β' = β - זוויות פנימיות מתחלפות a || AB , חותך AC.

3. 𝜶' + β' + ɣ = 180° - זוויות על הישר a.

4. 𝜶 + β + ɣ = 180° - נובע משוויונים 1, 2, 3.

מ.ש.ל.

היחס בין שטחי משולשים דומים שווה לריבוע יחס הדמיון בין המשולשים

קישורים:

גבהים מתאימים במשולשים דומים מתייחסים זה לזה כיחס הצלעות המתאימות.

חוצי זוויות מתאימות במשולשים דומים מתייחסים זה לזה כמו יחס הצלעות המתאימות.

תיכונים מתאימים במשולשים דומים מתייחסים זה לזה כיחס הצלעות המתאימות.

תיכונים מתאימים במשולשים דומים מתייחסים זה לזה כמו יחס הצלעות המתאימות

זוויות מתאימות במשולשים דומים מתייחסים זה לזה כמו יחס הצלעות המתאימות

משפט בגיאומטריה: אם במשולש חוצה זווית מתלכד עם הגובה ותיכון המשולש הוא שווה שוקיים

נתון

משולש ABC.

הקטע AO חוצה זווית A כך שזווית A1 שווה לזווית A2.

AO גם תיכון לצלע BC כך ש: BO=CO בנוסף AO אנך ל - BC.

משולש שבו חוצה זווית חוצה את הצלע ממול ומאונך לה

נדרש להוכיח כי משולש ABC שווה שוקיים: AB = BC

הוכחה: נוכיח ע"י חפיפת משולש AOB למשולש AOC ע"י ז.צ.ז.

זווית A1 = זווית A2 : נתון

AO = AO : צלע משותפת

זווית O1 = זווית O2 = זווית ישרה = 90 מעלות : נתון

מכאן משולשים AOB, AOC חופפים.

מהחפיפה נובע AB=AC ולכן משולש ABC שווה שוקיים.

מ.ש.ל

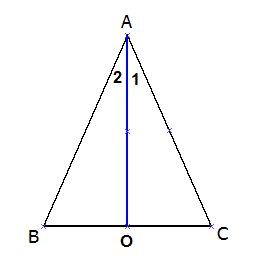משפט בגיאומטריה: זוויות הבסיס במשולש שווה שוקיים שוות

נתון משולש שווה שוקיים ABC שבו AB=AC.

משולש שווה שוקיים ABC שבו AB=AC

נדרש להוכיח כי הזווית B שווה לזווית C.

שיטת ההוכחה:
בונים בניית עזר את חוצה הזוית AO
כך ש: זוית A1 = זוית A2

מוכיחים כי המשולש AOC חופף למשולש AOB ע"פ צ.ז.צ:
AB=AC: נתון (משולש שווה שוקיים)
AO = AO : צלע משותפת.
זוית A1 = זוית A2 : מבניית העזר

מהחפיפה נובע כי זווית B שווה לזווית C
מ.ש.ל

רשימת משפטים בגיאומטריה

ישרים נחתכים

הוכחת משפט בגיאומטריה: עבור שני ישרים נחתכים כל שתי זוויות נגדיות (קודקודיות) שוות בגודלן
עבור שני ישרים נחתכים, סכום כל שתי זוויות סמוכות הוא 180º

ישרים מקבילים
אקסיומת המקבילים - אם שני ישרים ייחתכו על ידי ישר שלישי, באופן שסכום הזוויות הפנימיות שייווצרו באחד הצדדים קטן מסכום שתי זוויות ישרות (180 מעלות), אזי אם יוארכו הישרים מספיק באותו צד הם ייפגשו.

שני ישרים נחתכים על ידי ישר שלישי. אם יש זוג זוויות מתאימות שוות , אז שני הישרים מקבילים.
שני ישרים נחתכים על ידי ישר שלישי. אם יש זוג זוויות מתחלפות שוות אז שני הישרים מקבילים.
שני ישרים נחתכים על ידי ישר שלישי. אם סכום זוג זוויות חד-צדדיות הוא 180 מעלות אז שני הישרים מקבילים.

אם שני ישרים מקבילים נחתכים על ידי ישר שלישי אז:
א. כל שתי זוויות מתאימות שוות זו לזו.
ב. כל שתי זוויות פנימיות מתחלפות שוות זו לזו.
ג. סכום כל זוג זוויות חד-צדדיות הוא 180 מעלות.

.
משולשים
1. אם צלע אחת גדולה מצלע שנייה אז הזווית שמול הצלע הקטנה קטנה מהזווית שמול הצלע הגדולה

משפט הפוך: אם זוית אחת גדולה מזוית שניה אז הצלע שמול הזוית הקטנה, קטנה מהצלע שמול הזוית הגדולה
2. סכום כל שתי צלעות במשולש גדול מהצלע שלישית.
3. כל צלע במשולש גדולה מהפרש שתי הצלעות האחרות.
4. סכום הזויות במשולש 180 מעלות.

זווית חיצונית למשולש גדולה מכל אחת משתי הזוויות הפנימיות שאינן צמודות לה
5. זווית חיצונית למשולש שווה לסכום שתי הזויות הפנימיות שאינן צמודות לה.

חפיפת משולשים:
6. משפט חפיפה ראשון (אקסיומה): אם בשני משולשים שוות בהתאמה שתי צלעות והזווית שכלואה ביניהן המשולשים חופפים.
7. משפט חפיפה שני: אם בשני משולשים שוות בהתאמה שתי זוויות והצלע הכלואה ביניהן המשולשים חופפים.
משפט חפיפה שלישי: אם שלוש הצלעות במשולש אחד שוות בהתאמה לשלוש הצלעות במשולש שני אז המשולשים חופפים.
8. משפט חפיפה רביעי: אם בשני משולשים שוות בהתאמה שתי צלעות והזווית שמול הצלע הגדולה מביניהן המשולשים חופפים.
9. במשולשים חופפים מול צלעות שוות זוויות שוות.
10. במשולשים חופפים מול זוויות שוות צלעות שוות.

משולשים שווי שוקיים
11. זוויות בסיס במשולש שווה שוקיים שוות.
12. אם במשולש חוצה זווית מתלכד עם הגובה ותיכון המשולש הוא שווה שוקיים.
13. במשולש שווה שוקיים חוצה זווית הראש הוא גם גובה לבסיס, וחוצה את הבסיס (תיכון).
14. מול זוויות שוות במשולש צלעות שוות.
15. במשולש שווה שוקיים מרכז הבסיס נמצא במרחקים שווים מהשוקיים.
אם במשולש שני גבהים שווים זה לזה, אזי צלעות המשולש המאונכות לגבהים שוות

משולשים ישרי זווית
16. במשולש ישר זווית שזוויותיו החדות הן 30 ו- 60 מעלות, הניצב שמול הזוית 30 מעלות שווה למחצית היתר.
17. אם במשולש ישר זווית אחד הניצבים שווה למחצית היתר אז הזווית שמול הניצב שווה 30 מעלות.
18. במשולש ישר זווית התיכון ליתר שווה למחצית היתר.
19. משולש שבו אחד התיכונים שווה למחצית הצלע אותה הוא חוצה, הוא משולש ישר זווית.
20. הניצב במשולש ישר זווית הוא הממוצע הגיאומטרי של היתר והיטלו של ניצב זה על היתר.
21. אם הגובה לאחת הצלעות במשולש הוא הממוצע הגיאומטרי של היטלי שתי הצלעות האחרות על צלע זאת אז המשולש ישר זווית.
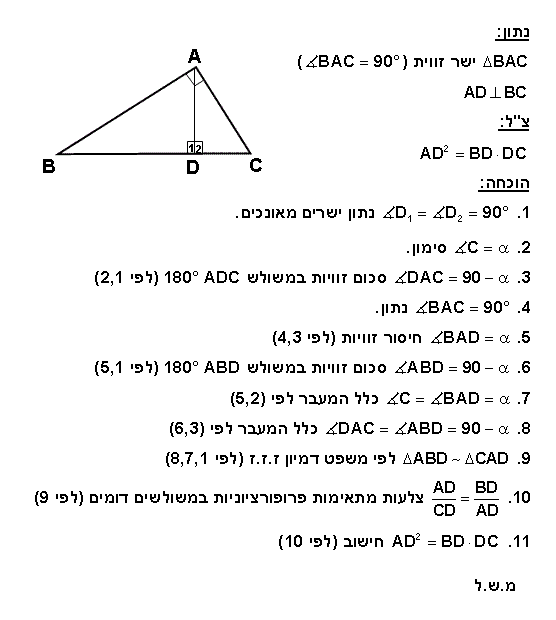הגובה ליתר במשולש ישר זווית הוא הממוצע הגאומטרי של היטלי הניצבים על היתר

משפט פיתגורס - במשולש ישר זוית סכום ריבוע הניצבים שווה לריבוע היתר
משפט פיתגורס ההפוך - אם במשולש סכום ריבועי שתי צלעות שווה לריבוע צלע שלישית אזי הזוית בין שתי הצלעות ישרה

קטע אמצעים במשולש
22. קטע אמצעים במשולש מקביל לצלע השלישית ושווה למחציתה.

24. קטע במשולש היוצא מאמצע צלע אחת ומקביל לצלע השלישית חוצה את הצלע השנייה.
25. קטע המחבר שתי צלעות במשולש, מקביל לצלע השלישית ושווה למחציתהּ הוא קטע אמצעים.

קטע אמצעים בטרפז
26. קטע אמצעים בטרפז מקביל לבסיסים ושווה למחצית סכומם.

28. האלכסון בטרפז שווה שוקיים גדול מקטע האמצעים.
29. קטע בטרפז היוצא מאמצע שוק אחת ומקביל לבסיסים חוצה את הצלע השנייה.

מרובעים

דלתון - מונחים ותכונות
האלכסון המשני בדלתון יוצר שני משולשים שווי שוקיים שבסיסם המשותף הוא האלכסון המשני
הזוויות הצדדיות בדלתון שוות זו לזו
האלכסון הראשי מחלק את הדלתון לשני משולשים חופפים
30. האלכסון הראשי בדלתון הוא חוצה זוויות הראש.
31. האלכסון הראשי בדלתון מאונך לאלכסון המשני וחוצה אותו.
32. שטח דלתון מחושב כמחצית מכפלת האלכסונים

33. סכום הזויות במרובע 360.

מקבילית
34. במקבילית כל זוג זוויות נגדיות שוות.
35. במקבילית האלכסונים חוצים זה את זה.
36. במקבילית כל זוג צלעות נגדיות שוות.
37. במקבילית כל זוג זוויות סמוכות סכומן 180.
38. אם במרובע כל זוג זווית נגדיות שוות המרובע הוא מקבילית.
39. אם במרובע כל זוג צלעות נגדיות שוות המרובע הוא מקבילית.
40. אם במרובע האלכסונים חוצים זה את זה המרובע הוא מקבילית.
41. אם במרובע קיים זוג צלעות נגדיות שוות ומקבילות אזי המרובע הוא מקבילית

42. במלבן האלכסונים שווים.

43. מקבילית שבה האלכסונים שווים זה לזה היא מלבן.

מעוין - הגדרה: מעוין הוא מרובע שווה צלעות
44. אלכסוני המעוין חוצים את זוויות המעוין.
45. אלכסוני המעוין מאונכים זה לזה.
46. מקבילית שבה האלכסונים מאונכים זה לזה היא מעוין.
צלעות נגדיות במעוין מקבילות
זוויות נגדיות במעוין שוות זו לזו
אלכסוני המעוין חוצים זה את זה
הגבהים במעוין שווים באורכם

מקבילית שבה אלכסון חוצה את הזווית היא מעוין.
מקבילית עם זוג צלעות סמוכות שוות היא מעוין.

בכל מעוין ניתן לחסום מעגל

טרפז שווה שוקיים
47. זוויות הבסיס בטרפז שווה שוקיים שוות.
48. בטרפז שווה שוקיים האלכסונים שווים.
אם האלכסונים בטרפז שווים זה לזה אז הוא טרפז שווה שוקיים
האלכסונים יוצרים עם הבסיסים משולשים שווי-שוקיים

מעגלים
49. למיתרים שווים מתאימות קשתות שוות ולהיפך.
50. שלוש נקודות הנמצאות על מעגל אחד אינן יכולות להימצא על ישר אחד.
51. שלוש נקודות שאינן על ישר אחד קובעות מעגל אחד ויחיד.
52. לקשתות שוות מתאימות זוויות מרכזיות שוות.
53. לזוויות מרכזיות שוות מתאימות קשתות שוות.
54. למיתרים שווים מתאימות זוויות מרכזיות שוות.
55. לזוויות מרכזיות שוות מתאימים מיתרים שווים.
56. אנך מהמרכז למיתר במעגל חוצה את המיתר, חוצה את הזווית המרכזית המתאימה ואת הקשת המתאימה.
57. קטע ממרכז המעגל החוצה את המיתר מאונך למיתר.
58. אנך מאמצע המיתר עובר דרך מרכז המעגל.
59. מיתרים שווים במעגל נמצאים במרחקים שווים מהמרכז.
60. מיתרים במעגל הנמצאים במרחקים שווים מהמרכז שווים זה לזה.
61. אם במעגל, מיתר אחד גדול ממיתר שני, אז מרחקו מהמרכז של המיתר הראשון קטן ממרחקו של השני.
62. הזווית המרכזית במעגל גדולה פי 2 מכל זווית היקפית הנשענת על אותה קשת.
63. כל הזוויות ההיקפיות הנשענות על אותה קשת שוות זו לזו.
64. זווית היקפית הנשענת על קוטר שווה ל- 90 מעלות.
65. זוויות היקפיות שוות- נשענות על מיתרים (קשתות) שווים.
66. על מיתרים (קשתות) שווים נשענות זוויות היקפיות שוות או שסכומן 180 מעלות.
67. זווית פנימית במעגל שווה לסכום שתי הזוויות ההיקפיות הנשענות על הקשתות הכלואות בין שוקי הזווית והמשכיהן.
68. זווית פנימית שווה למחצית סכום הקשתות שנשענות על שוקי הזווית ועל המשכיהן.
69. זווית חיצונית למעגל שווה להיפרש שבין שתי הזוויות ההיקפיות הנשענות על אותה קשת.

משיק למעגל
70. משיק למעגל מאונך לרדיוס העובר בנקודת ההשקה.
71. ישר המאונך לרדיוס בקצהו משיק למעגל
72. שני משיקים למעגל היוצאים מאותה נקודה שווים זה לזה
73. הזווית בין משיק למיתר הנפגשים בנקודת ההשקה שווה לזווית ההיקפית הנשענת על המיתר מצידו השני.
אם מנקודה שמחוץ למעגל יוצאים שני משיקים למעגל, אז הקטע המחבר את מרכז המעגל עם הנקודה שממנה יוצאים שני המשיקים חוצה את הזווית שבין המשיקים.

74. נקודת המגע של שני מעגלים משיקים נמצאת על קטע המרכזים או על המשכו.
75. מרכז המעגל החוסם את המשולש הוא מפגש האנכים האמצעיים לצלעות.
76. מרכז המעגל החסום במשולש הוא מפגש חוצי הזווית.
77. כל זוג זוויות נגדיות במרובע חסום במעגל סכומן 180 מעלות.
78. במרובע חוסם מעגל סכום זוג אחד של צלעות נגדיות שווה לסכום הזוג השני.
79. מרובע שבו סכום זוג צלעות נגדיות שווה לסכום הזוג השני הוא מרובע חוסם מעגל.
80. אם מחלקים מעגל לn קשתות שוות ומחברים את נקודות החלוקה בזו אחר זו מקבלים מצולע משוכלל בעל n קשתות.
81. כל מצולע משוכלל אפשר לחסום במעגל.
82. בכל מצולע משוכלל אפשר לחסום מעגל.
83. שני מיתרים, הנחתכים במעגל, מחלקים זה את זה כך שמכפלת קטעי מיתר אחד שווה למכפלת קטעי המיתר השני.
84. אם למעגל יוצאים שני חותכים מאותה נקודה אז מכפלת חותך אחד בחלקו החיצוני שווה למכפלת החותך השני בחלקו החיצוני.
85. אם מנקודה מחוץ למעגל יוצאים חותך ומשיק למעגל אז מכפלת החותך בחלקו החיצונה זהו גודל קבוע השווה לריבוע המשיק.

שטחים

86. שטח המלבן שווה למכפלת צלע אחת בצלע שנייה.
87. שטח מקבילית שווה למכפלת צלע בגובה שלה.
88. שטח משולש שווה למחצית המכפלה של צלע בגובה שלה.
89. שטח טרפז שווה למחצית המכפלה של סכום הבסיסים בגובה.
90. שטחי מעוין, ריבוע ודלתון שווים למחצית מכפלת אלכסוניהם.

פרופורציה

91. כל שני תיכונים במשולש מחלקים זה את זה לשני קטעים כך שהקטע הקרוב לקודקוד גדול פי שניים מהקטע הקרוב לצלע.
92. משפט תאלס - שני ישרים מקבילים החותכים שוקי זווית מקצים עליהן קטעים פרופורציונים.
93. משפט תאלס ההפוך: שני ישרים המקצים על שוקי זוית קטעים פרופורציונים – מקבילים זה לזה.
94. משפט חוצה זווית - חוצה זווית במשולש מחלק את הצלע שמול הזווית לשני קטעים המתייחסים זה לזה כמו היחס שבין הצלעות הכולאות את הזווית.
95. משפט חוצה זוית הפוך: קטע המחבר קודקוד במשולש עם הצלע שמולו ומחלק אותה לשני קטעים המתייחסים זה לזה כמו היחס שבין שתי הצלעות האחרות- חוצה את זווית המשולש.
96. ישר המקביל לצלע של משולש חותך ממנו משולש הדומה לו.

דמיון משולשים

97. אם בשני משולשים קיים יחס שווה בין שני זוגות צלעות מתאימות והזווית שביניהן שווה בהתאמה אז המשולשים דומים.
98. אם בשני משולשים שוות בהתאמה שתי זוויות המשולשים דומים.
99. אם בשני משולשים קיים יחס שווה בין שלושת זוגות הצלעות המתאימות אז המשולשים דומים.
100. אם בשני משולשים קיים יחס שווה בין שני זוגות של צלעות מתאימות והזוויות שמול הצלע הגדולה מהשתיים שוות בהתאמה אז המשולשים דומים.
101. גבהים מתאימים במשולשים דומים מתייחסים זה לזה כיחס הצלעות המתאימות.
102. חוצי זוויות מתאימות במשולשים דומים מתייחסים זה לזה כמו יחס הצלעות המתאימות.
103. תיכונים מתאימים במשולשים דומים מתייחסים זה לזה כיחס הצלעות המתאימות.
104. הרדיוסים של מעגלים החוסמים משולשים דומים מתייחסים זה לזה כיחס הצלעות המתאימות.
105. הרדיוסים של מעגלים החסומים במשולשים דומים מתייחסים זה לזה כמו יחס הצלעות המתאימות.
106. ההיקפים של משולשים דומים מתייחסים זה לזה כמו יחס הצלעות המתאימות.
107. שטחים של משולשים דומים מתייחסים זה לזה כריבוע היחס שבין הצלעות המתאימות.
108. הגובה ליתר במשולש ישר זווית מחלק את המשולש לשני משולשים דומים שכל אחד דומה למשולש המקורי.
109. הגובה ליתר במשולש ישר זווית הוא הממוצע הגיאומטרי של היטלי הניצבים על היתר.

אחר
110. זוויות קודקודיות תמיד שוות.
111. אם מנקודה מחוץ לישר יוצאים שני קטעים משופעים שווים אז גם היטליהם שווים וההיפך.
112. אם היטלו של משופע אחד גדול מהיטלו של משופע שני אז המשופע הראשון גדול מהמשופע השני.
113.
114. שני גדלים השווים לגודל שלישי שווים ביניהם.
115. אם מחברים גדלים שווים לגדלים שווים הסכומים שווים.
116. אם מחסרים גדלים שווים מגדלים שווים מגדלים שווים אז ההפרשים שווים.
117. אם מחלקים גדלים שווים בגדלים שווים המנות שוות.
118. אם כופלים גדלים שווים בגדלים שווים המכפלות שוות.
119. אם שתי זווית במשולש שוות לשתי זוויות במשולש אחר אז הזווית השלישית שווה.
120. משלימות אותן זוויות ל180.
121. בתבניות ניתן להציב גודל מסוים במקום גודל השווה לו.
122. זוויות צמודות סכומן 180.
123. דרך נקודה הנמצאת מחוץ לישר נתון ניתן להעביר ישר אחד ויחיד המקביל לישר הנתון.
124. סכום הזויות החיצוניות במצולע 360.
125. כל נקודה על האנך האמצעי נמצאת במרחקים שווים מקצות הקטע.
126. כל נקודה הנמצאת במרחקים שווים מקצות הקטע נמצאת על האנך האמצעי.
127. כל נקודה הנמצאת על חוצה הזווית נמצאת במרחקים שווים משוקי הזווית.
128. כל נקודה הנמצאת על במרחקים שווים משוקי הזווית נמצאת על חוצה הזווית.
129. שלושת התיכונים במשולש נפגשים בנקודה אחת.
130. שלושת הגבהים במשולש נפגשים בנקודה אחת.
שלושת חוצי הזוויות במשולש נפגשים בנקודה אחת
שלושת האנכים האמצעיים לצלעות המשולש נפגשים בנקודה אחת
כל שני אנכים אמצעיים לצלעות במשולש נחתכים
131. שטח ריבוע שצלעו ניצב אחד של משולש ישר זווית שווה לשטח מלבן שצלעותיו הן היתר וההיטל של ניצב זה על היתר. (משפט אוקלידס)
132. בכל משולש ישר זווית סכום שטחי הריבועים הבנויים על הניצבים שווה לשטח הריבוע הבנוי על היתר. (משפט פיתגורס)